Zeichne dir mal die Kosinusfunktion y = cos(x) auf:
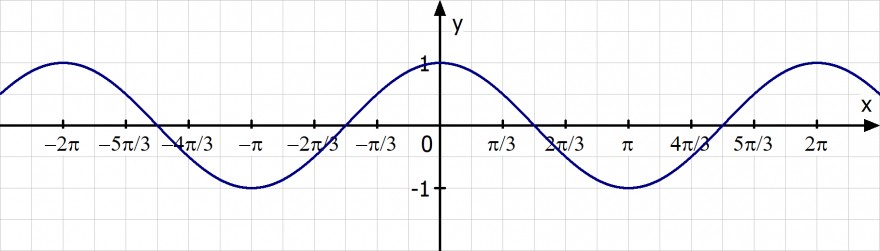
Was fällt dir auf?
Die Nullstellen liegen alle voneinander im Abstand von pi zueinander und es gibt unendlich viele.
Weiterhin wird die Cosinusfunktion immer im Bogenmaß gerechnet. . D.h. nicht mit Winkeln im Gradmaß sondern eben im Bogenmaß. Denn nur dann ist die Ableitung vom Sinus der Cosinus.