Hallo,
Arbeit ist Kraft mal Weg. Genauer: Arbeit ist das Skalarprodukt aus dem Kraft- und dem Wegvektor. Und die Summe aller kleinen Arbeiten, wenn die Kraft vom Weg abhängt, ist$$W = \int \text dW = \int \left< \vec F,\, \text d\vec s\right>$$die Länge eines Weges im Raum folgt aus Pythagoras$$\left(\text d\vec s\right)^2 = \text dx^2 + \text dy^2 + \text dz^2$$und mit der Geradengleichung$$\vec g(t) = A(1-t) + Bt = A + (B-A)t \\ \phantom{\vec g(t)} = A + \vec r t = \begin{pmatrix} 1\\1\\0 \end{pmatrix} + \begin{pmatrix} -1\\1\\3 \end{pmatrix}t$$und ihrer Ableitung nach \(t\)$$\frac{\vec g(t)}{\text dt} = \begin{pmatrix} \text dx/\text dt\\\text dy/\text dt\\\text dz/\text dt \end{pmatrix} = \begin{pmatrix} -1\\1\\3 \end{pmatrix} = \vec r$$kann man nun schreiben$$\left(\text d\vec s\right)^2 = |\vec r|^2\, \text dt^2$$Wir benötigen aber eine gerichtetes \(\text d\vec s\), daher multipliziere ich das nach dem Ziehen der Wurzel mit dem Einheitsvektor von \(\vec r\) und erhalte$$\text d\vec s = \frac{\vec r}{|\vec r|} \sqrt{|\vec r|^2}\, \text dt = \vec r\, \text dt$$Oben in das Integral einsetzen mit \(\vec F = 2\vec x\) gibt dann$$\begin{aligned} W &= \int \left< \vec F,\, \text d\vec s\right>\\ &= \int_0^1 2 \left< \vec x, \, \vec r\right> \text dt &&|\, \vec x = \vec g(t) \\ &= 2 \int_0^1 \left< A + \vec r t,\, \vec r\right>\, \text dt \\ &= 2\left[A \vec r t + \frac 12\vec r^2 t^2 \right]_0^1 \\&= 2A\vec r + \vec r^2 \\&= 11\end{aligned}$$Zur Veranschaulichung ein Bild
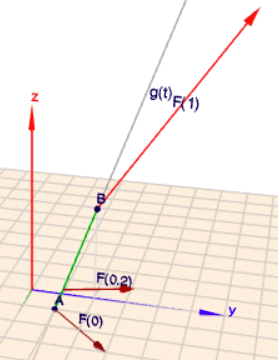
(klick auf das Bild, dann kannst Du die Szene mit der Maus rotieren und bekommst einen besseren Eindruck)
Gruß Werner