Extrempunkte und Nullstellen ermitteln

Question

Aufgabe:

Die Funktionen fa(x)= 1/a2 * x3 -6/a * x2+9x (a>0) ist gegeben

Ermitteln Sie die Extrempunkte und Nullstellen der Funktion fa(x)

Answer 1

Hallo

lesbar: fa(x)= 1/a^2 * x^3 -6/a * x^2+9*x

was hindert dich daran das zu differenzieren, und dann f'(x)=0

eine quadratische Gleichung zu lösen mit a als Parameter kann dich doch wohl nicht überfordern? Tip: die entstehende quadratische Gleichung mit a^2/3 multiplizieren.

Gruß lul

Answer 2

fa(x)= \( \frac{1}{a^2} \) * x^3 -\( \frac{6}{a} \) * x^2+9x mit  a>0

Nullstellen:

\( \frac{1}{a^2} \) * x^3 -\( \frac{6}{a} \) * x^2+9x=0

x(\( \frac{1}{a^2} \) * x^2 -\( \frac{6}{a} \) * x+9)=0

x₁=0

\( \frac{1}{a^2} \) * x^2 -\( \frac{6}{a} \) * x+9=0|*a^2

x^2 - 6 a x+9 a^2=0

x^2 - 6 a x = - 9 a^2

(x-3a)^2=- 9 a^2+9a^2=0

x-3a=0

x=3a (doppelte Nullstelle, Extremwert)

Extremwerte:

f´a(x)= \( \frac{3}{a^2} \) * x^2 -\( \frac{12}{a} \) * x+9

\( \frac{3}{a^2} \) * x^2 -\( \frac{12}{a} \) * x+9=0|:\( \frac{3}{a^2} \)

x^2 - 4 a* x=-3a^2

(x-2a)^2=-3a^2+4a^2=a^2|\( \sqrt{} \)

1.) x=2a+a=3a (siehe Nullstelle)

2.)x=2a-a=a    f(a)= \( \frac{1}{a^2} \) * a^3 -\( \frac{6}{a} \) * a^2+9a=a-6a+9a=4a

Art der Extremwerte:

f´´a(x)= \( \frac{6}{a^2} \) * x -\( \frac{12}{a} \) 

f´´a(3a)= \( \frac{6}{a^2} \) * 3a -\( \frac{12}{a} \)=\( \frac{6}{a} \)  >0  Minimum

f´´a(a)= \( \frac{6}{a^2} \) * a -\( \frac{12}{a} \)=-\( \frac{6}{a} \)<0  Maximum

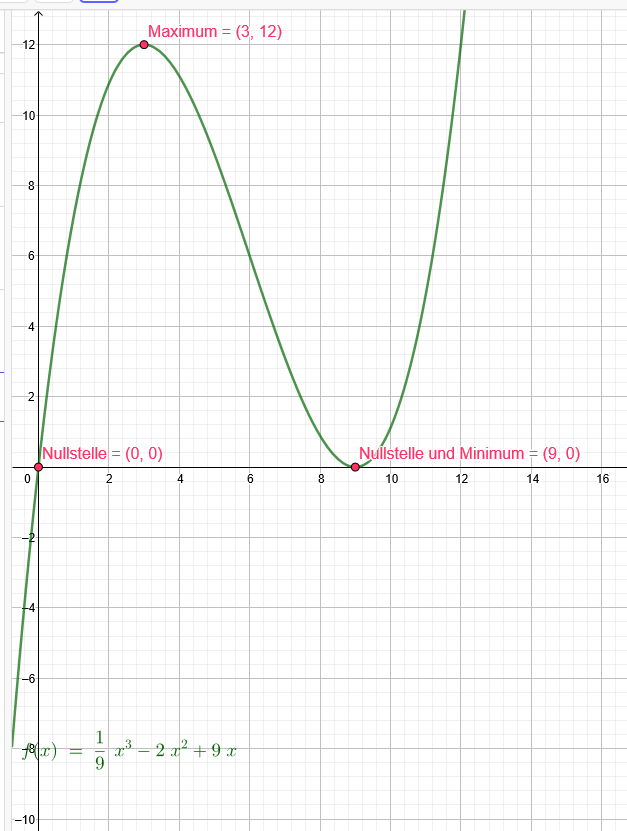
Zeichnung mit a=3