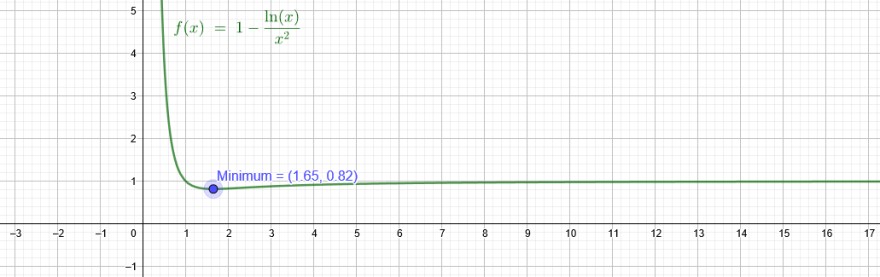
Nullstellen und Extrempunkte des Graphen von f berechnen:
f(x) = 1-\( \frac{ln(x)}{x^2} \)
Ich forme um:
f(x) =\( \frac{x^2-ln(x)}{x^2} \)
Nullstellen: Zähler =0
\( x^{2} \)-ln(x)=0
\( x^{2} \)=ln(x) Es gibt keinen Schnittpunkt in ℝ. → keine Nullstellen
Extrempunkte:

Text erkannt:
\( f(x)=\frac{x^{2}-\ln (x)}{x^{2}} \)
\( f \cdot(x)=\frac{\left(2 x-\frac{1}{x}\right) \cdot x^{2}-\left(x^{2}-\ln (x)\right) \cdot 2 x}{x^{4}}=\frac{\left(2 x-\frac{1}{x}\right) \cdot x-2 x^{2}+2 \ln (x)}{x^{3}} \)
\( f^{\prime}(x)=\frac{2 \ln (x)-1}{x^{3}} \)
\( \frac{2 \ln (x)-1}{x^{3}}=0 \)
\( 2 \ln (x)=1 \)
\( \ln (x)=\frac{1}{2} \)
\( e^{\ln (x)}=e^{\frac{1}{2}} \)
\( x=e^{\frac{1}{2}} \rightarrow \rightarrow f\left(e^{\frac{1}{2}}\right)=\frac{\left(e^{\frac{1}{2}}\right.}{\text { Art des Extremwertes: }} \)
Art des Extremwertes:
\( f \cdot(x)=\frac{\left(\frac{2}{x}\right) \cdot x^{3}-(2 \ln (x)-1) \cdot 3 x^{2}}{x^{6}}=\frac{\left(\frac{2}{x}\right) \cdot x-(2 \ln (x)-1) \cdot 3}{x^{4}}=\frac{5-6 \ln (x)}{x^{4}} \)
\( f \cdot\left(e^{\frac{1}{2}}\right)=\frac{5-6 \ln \left(e^{\frac{1}{2}}\right)}{e^{2}}=\frac{2}{e^{2}}>0 \rightarrow \text { Minimum } \)