Aufgabe:
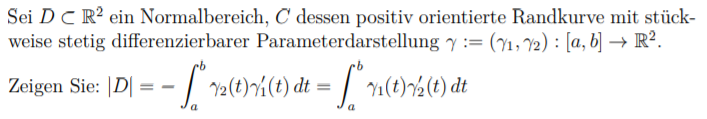
Text erkannt:
Sei \( D \subset \mathbb{R}^{2} \) ein Normalbereich, \( C \) dessen positiv orientierte Randkurve mit stückweise stetig differenzierbarer Parameterdarstellung \( \gamma:=\left(\gamma_{1}, \gamma_{2}\right):[a, b] \rightarrow \mathbb{R}^{2} \). Zeigen Sie: \( |D|=-\int \limits_{a}^{b} \gamma_{2}(t) \gamma_{1}^{\prime}(t) d t=\int \limits_{a}^{b} \gamma_{1}(t) \gamma_{2}^{\prime}(t) d t \)
Kann mir jemand da einen Tipp geben?