Hallo,
Um Schreibarbeit zu sparen, setze ich$$a= \vec{A'D'},\,b=\vec{A'B'},\, c=\vec{A'A} $$und ich wähle drei Variablen$$\alpha,\,\beta,\,\gamma \in \mathbb R$$mit denen ich die Punkte \(R\), \(S\) und \(T\) beschreiben kann. Es ist$$\vec{A'R} = \alpha a\\ \vec{A'S} = a + \beta c \\ \vec{A'T} = b+c+\gamma a$$Das Viereck ist natürlich nur dann ein Parallelogramm, wenn es eben ist. Den vierten Punkt eines Parallelogramms kann man aus den dreien berechnen. Ich nenne den vierten Punkt \(S^*\) dann ist $$\vec{A'S^*} = \vec{A'R} + \vec{A'T} - \vec{A'S} \\ \phantom{\vec{A'S^*}}= (\alpha + \gamma) a + b+c - (a + \beta c) \\ \phantom{\vec{A'S^*}}= (\underbrace{\alpha + \gamma -1}_{=0}) a + b+(1-\beta)c$$Mit der Bedingung, dass \(U\) auf \(BB'\) liegen muss, folgt, dass der Faktor vor \(a\) gleich 0 ist. Weiter muss der Faktor vor \(b\) gleich \(1\) sein. Dies ist aber immer erfüllt.
Und damit ist gezeigt, dass auf \(BB'\) ein Punkt \(U=S^*\) existiert, so dass \(RSTU\) ein Parallelogramm ist.
Nachtrag: damit ein Parallelogramm vorliegt muss also \(\alpha + \gamma = 1\) sein, das bedeutet, dass \(|A'R|=|TC|\) sein muss. Und wenn man den Punkt \(U\) auf \(BB'\) mit $$\vec{A'U} = b + \delta c, \quad \delta \in \mathbb R$$bezeichnet, dann muss $$b + \delta c = b+(1-\beta)c \\ \implies \delta + \beta = 1$$sein. D.h. \(|SD'|=|BU|\).
Ohne diese Bedingung ließen sich auf den Kanten des Spats auch andere Vierecke realisieren. Wie hier zu sehen ist:
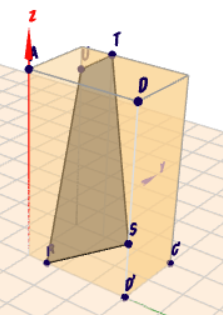
(klick auf das Bild)