Stetigkeit, wo ist die Funktion stetig?

Question

Aufgabe:

An welchen Stellen ist die Funktion stetig, an welchen nicht? Skizzieren sie den Graphen der Funktion.

f(x) = { 0, x=0

{ \( \frac{πx}{|x|} \) , x≠0 und x<1

{ arccos(x-2), 1 ≤ x ≤ 2

{ arcsin (\( \frac{2}{x} \)) , x>2

(Geschweifte Klammer soll eigentlich ein großes sein)

Problem/Ansatz:

Ich verzweifle schon den ganzen Tag an dieser Aufgabe und bin immer noch am selben Punkt wie am Anfang. Ich verstehe einfach nicht, wie ich vorgehen muss. Kann mir Jemand helfen, die Aufgabe zu lösen?

Answer 1

Hallo

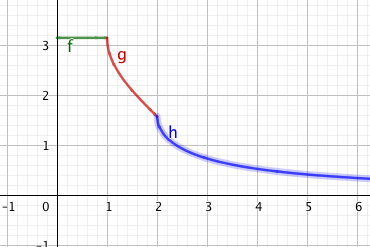
bevor man verzweifelt skizzierst man mal die Funktion, oder lässt ein Programm sie plotten.

Dann sieht man direkt, dass sie überall stetig ist ausser bei x=0 wo sie von 0 auf pi springt.

Dann muss man nur die Übergangsstellen also x=0, 1, 2 betrachten, da an allen anderen Stellen einfach stetige Funktionen stehen

also betrachte an diesen Stellen jeweils den GW der einen Funktion bei der < steht oder >   mit dem Funktionswert bei =

wenn sie übereinstimmen, wie bei 1 und 2 ist die Funktion dort stetig, sonst  wie bei 0 nicht.

Gruß lul