Hallo Clara,
Willkommen in der Mathelounge!
Wähle auf dem Kreis drei Punkte \(A\), \(B\) und \(C\)
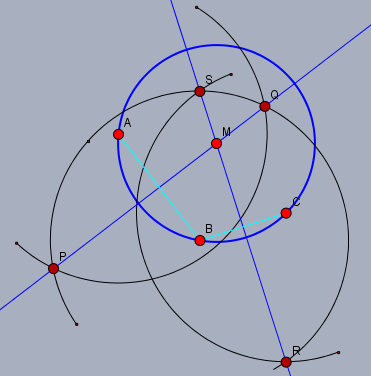
dann schlage mit dem Zirkel mit genau einem Radius einen Kreis um jeden der drei Punkte. Der Radius muss nur ausreichend groß sein, so dass sich die Kreise auch schneiden. Die Kreise um \(A\) und \(B\) schneiden sich in \(P\) und \(Q\) und die Kreise um \(B\) und \(C\) schneiden sich in \(R\) und \(S\). Die Geraden \(g\) durch \(PQ\) und \(h\) durch \(RS\) schneiden sich im Mittelpunkt \(M\) des Kreises.
\(g\) und \(h\) sind die sogenannten Mittelsenkrechten der Strecken \(AB\) und \(BC\) (hellblau). Jeder Punkt auf einer Mittelsenkrechten ist von den beiden Endpunkten der Strecke gleich weit entfernt. Für den Schnittpunkt \(M\) bedeutet dies, dass die Distanz \(|AM|=|BM|\) ist, da \(M\) auf \(g\) liegt und auch \(|BM|=|CM|\) ist, da \(M\) auch auf \(h\) liegt.
Folglich ist \(|AM|=|BM|=|CM|\) und \(M\) muss somit der Mittelpunkt des Kreises sein, der durch diese drei Punkte verläuft.
Gruß Werner