Winkelgleichheit eines Dreiecks im Kreis beweisen

Question

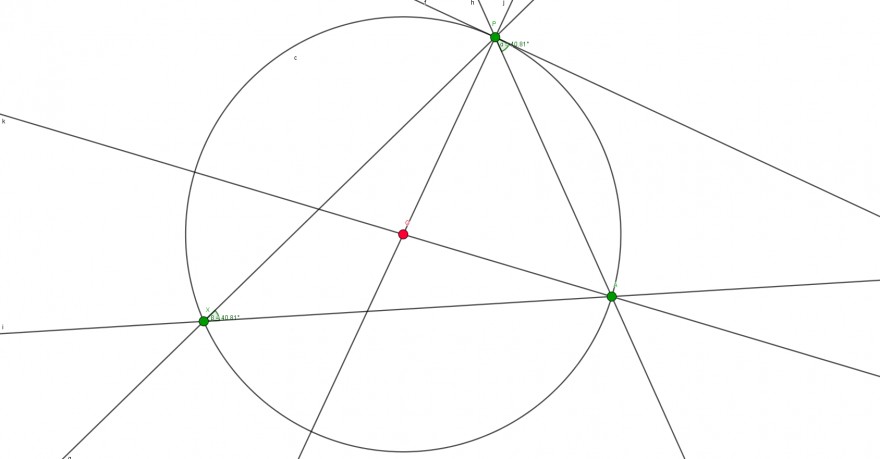
Aufgabe:

Ich würde gerne in der Situation der Skizze zeigen, dass der Winkel α gleich dem Winkel β ist.

(Der Winkel α verlässt den Kreis minimal weil er bis zur Tangente aufgezogen ist, sieht man in der Skizze leider nicht gut)

Problem/Ansatz:

Geogebra zeigt mir schon mal, dass die Winkel offensichtlich gleich sind, jedoch weiß ich leider nicht wie ich das beweisen soll.

Ich weiß, dass es sich bei der Strecke PA und PX um eine Sehne des Kreises mit Mittelpunkt O handelt.

Mein ursprünglicher Plan war vlt. mit einem Sehnenviereck zu arbeiten, da ich dort verwenden darf, dass gegenüberliegen Winkel sich zu 180° ergänzen, jedoch hab ich nach ein wenig herumprobieren keinen Weg gefunden die Aussage damit zu beweisen. (Weil der Winkel am Punkt P, den Kreis theoretisch verlässt, je nach Tangente, und ich das berücksichten muss, ist ein Sehnenviereck daher unbrauchbar.)

Kann mir hier jemand weiterhelfen?

Gruß Spiegel

Answer 1

Hallo,

ich kann die Bezeichnungen der Punkte in Deiner Skizze leider nicht lesen. Daher hier die Skizze noch einmal:

Der Mittelpunktswinkel \(\gamma = \angle QMP\) (gelb) ist doppelt so groß wie der Umfangswinkel \(\alpha=\angle QXP\) (blau) (Kreiswinkelsatz). Das Dreieck \(\triangle QMP\) ist gleichschenklig. Folglich sind seine Basiswinkel \(\delta\) $$\delta = \frac 12 \left( 180° - \gamma \right) = \frac 12(180° - 2 \alpha) = 90° - \alpha$$Ein Basiswinkel und der Winkel \(\beta\) (grün) ergeben \(90°\)$$\begin{aligned} \beta + \delta &= 90° \\ \beta &= 90° - \delta = 90° - (90° - \alpha) = \alpha \end{aligned}$$Falls etwas unklar ist, so frage bitte nach.

Gruß Werner

Comments

Vielen Dank für dein super verständliche Antwort!!

Gruß,

Spiegel