Konstruktionsproblem im R^2

Question

Aufgabe:

Ich muss aus der Menge {(0,0),(0,1),(1,0)} in (R^2, d2) zwei Punkte x,y (Element von R^2) im Abstand von \( \frac{1+\sqrt{5}}{4} \) konstruieren.

Problem/Ansatz:

Leider habe ich keinerlei Idee, wie man genau auf die beiden Punkte kommen könnte. Ich habe es echt lange versucht, aber ich komme nicht auf diese Punkte.

Comments

\( \frac{1-√5}{4} \) kann kein Abstand sein, weil Abstände grundsätzlich positiv sind.

Answer 1

Hallo Oli,

die Konstruktion einer Strecke \((1+\sqrt 5)/4\) mit Zirkel und Lineal geht wie folgt:

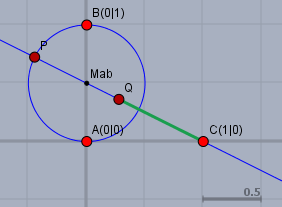
Es sei \(A=(0|\,0)\), \(B=(0|\,1)\) und \(C=(1|\,0)\).

Konstruiere die Mitte \(M_{ab}\) der Strecke \(AB\) (ich nehme an, Du weißt wie das geht). Zeichne einen Kreis um \(M_{ab}\) mit Radius \(M_{ab}A\). Die Gerade durch \(M_{ab}C\) schneidet den Kreis in \(P\), wobei \(P\) außerhalb der Strecke \(M_{ab}C\) liegt. Konstruiere die Mitte \(Q\) der Strecke \(PC\).

Die Strecke \(|QC|\) hat die Länge \((1+\sqrt 5)/4\).

Zur Erklärung: die Strecke \(|M_{ab}C|\) ist lt. Pythagoras$$|M_{ab}C| = \sqrt{1^2 + \left(\frac 12\right)^2} = \frac 12 \sqrt 5$$und demzufolge ist$$|PC| = |PM_{ab}| + |M_{ab}C| = \frac 12 + \frac 12 \sqrt 5 = \frac{1 + \sqrt 5}2$$und \(|QC|\) ist halb so lang.

Gruß Werner

Comments

Super!! Vielen vielen herzlichen Dank und beste Grüße!

Answer 2

Da kann man nur raten

wie lautet die Aufgabe im Original?

Comments

Aber falls ich nur folgende Kreise konstruieren kann:

Den Kreis um A mit dem Radius der Strecke AB

Den Kreis um B mit dem Radius der Strecke AB oder BC

Den Kreis um C mit dem Radius der Strecke AC oder BC

Dann funktioniert es doch nicht oder? Hab die gleiche Konstruktion gerade auf Papier versucht aber der Abstand ist nicht, wie er sein soll.

Hätten Sie da eine Lösung? Oder habe ich mich einfach vertan?

---

Nochmal: Originaltext!

Ich habe den Abstand als Radius der Kreise eingesetzt - die Aufgabenstellung ist unverständlich / zumindest interpretationsabhängig ...

---

Die Aufgabenstellung ist original so:

Konstruieren Sie in (R²,d₂) zwei Punkte x,y (Element von R²) mit Abstand d₂(x,y)=\( \frac{1+\sqrt{5}}{4} \) mit Zirkel und Lineal aus der Menge {(0,0),(0,1),(1,0)}.