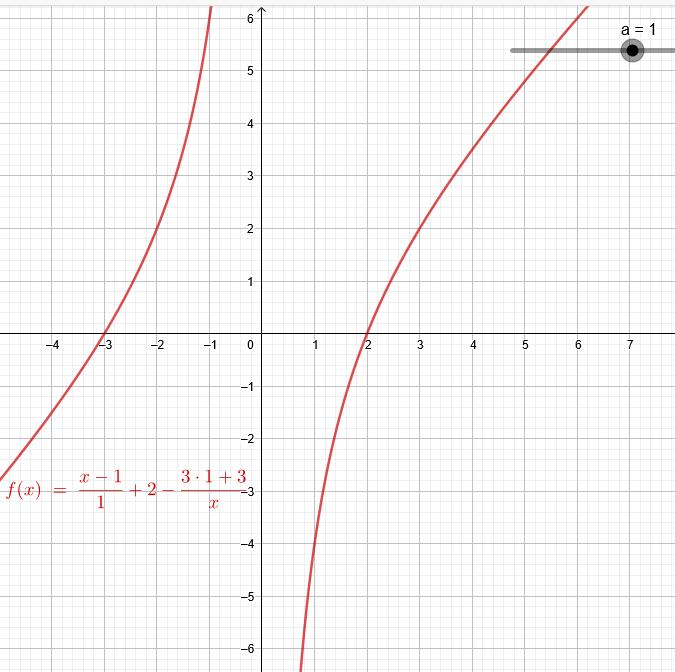
\( \frac{x-1}{a} \)+2=\( \frac{3a+3}{x} \)|*ax Definitionsmenge : alle x mit x≠0 und a ≠0
(x-1)*x+2ax=(3a+3)*a
\( x^{2} \)-x+2ax=3a^2+3a
\( x^{2} \)+x*(2a-1)=3a^2+3a
(x+\( \frac{2a-1}{2} \))^2=3a^2+3a+\( \frac{(2a-1)^2 }{4} \)=\( \frac{12a^2+12a+4a^2-4a+1}{4} \)=\( \frac{16a^2+8a+1}{4} \)=\( \frac{1}{4} \)*(16a^2+8a+1)|\( \sqrt{} \)
1.)x+\( \frac{2a-1}{2} \)=\( \frac{1}{2} \)*\( \sqrt{16a^2+8a+1} \)
x₁=-a+\( \frac{1}{2} \)+\( \frac{1}{2} \)*\( \sqrt{16a^2+8a+1} \)
2.)x+\( \frac{2a-1}{2} \)=-\( \frac{1}{2} \)*\( \sqrt{16a^2+8a+1} \)
x₂=-a-\( \frac{1}{2} \)-\( \frac{1}{2} \)*\( \sqrt{16a^2+8a+1} \)