Hallo Alex,
es ginge einfacher, wenn Du Dir das aufzeichnest:
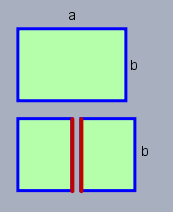
Du sieht oben das ursprüngliche Rechteck mit der langen Seite \(a\) und der kurzen \(b\). Der blaue Umfang ist \(80\,\text{cm}\). Wenn man das Rechteck wie beschrieben teilt, dann bleiben die blauen Seiten alle erhalten und es kommen zwei Seiten (rot) der Länge \(b\) hinzu. Die Summe der Umfänge der beide kleineren Rechtecke ist \(2 \cdot 56\text{cm} = 112\,\text{cm}\).
Folglich ist die Differenz der Umfänge genau so groß wie \(2b\):$$\begin{aligned} 2b &= 112 - 80 \\ 2b &= 32 &&|\,\div 2\\ b &= 16 \end{aligned}$$Und da der ursprüngliche Umfang \(80\,\text{cm}\) war, gilt$$\begin{aligned}2a+ 2b &= 80 \\ 2a + 2\cdot 16 &= 80 &&|\, -32\\ 2a &= 48 &&|\,\div 2 \\ a &= 24\end{aligned}$$
1.Gleichung 80= 2a+2b
das war richtig
2.Gleichung U=2a+2b
56=2a+2b
das ist nicht richtig, da die eine Seite des kleineren Rechtecks nicht mehr \(a\) ist, sondern halbiert wurde, also \(a/2\). Es muss heißen$$56 = 2\cdot\left( \frac a2\right) + 2b$$Umformen nach \(a\) gibt$$a = 56 - 2b$$ und einsetzen in die erste Gleichung$$\begin{aligned}80 &= 2(56 - 2b) + 2b \\ 80 &= 112 - 4b + 2b \\ 80 &= 112 - 2b &&|\,+2b \\ 80 + 2b &= 112 &&|\,-80\\ 2b &= 112 - 80\end{aligned}$$... und dann bist Du bei der Gleichung angekommen, die ich oben schon geschrieben habe.
Gruß Werner