Aufgabe:
Brauche Lösung mit weg
Problem/Ansatz:
Text erkannt:
Ernteertrag
Ein Landwirt will den Ertrag pro Quadratmeter für eine bestimmte Gemüsesorte steigern. Dazu prüft er den Einsatz eines Düngemittels.
a) Die Ableitungsfunktion \( E^{\prime} \) der Ertragsfunktion \( E \) lautet:
\( E^{\prime}(x)=-891 \cdot x^{2}+297 \cdot x \) mit \( 0 \leq x \leq 0,53 \)
\( x \)... Düngermenge in \( \mathrm{kg} / \mathrm{m}^{2} \) \( E^{\prime}(x) \)... lokale Ertragsänderungsrate des Ertrags bei der Düngermenge \( x \)
Ohne Düngemittel erntet der Landwirt durchschnittlich \( 2,5 \mathrm{~kg} \) Gemüse pro Quadratmeter
- Ermitteln Sie die Funktionsgleichung der Ertragsfunktion \( E \).
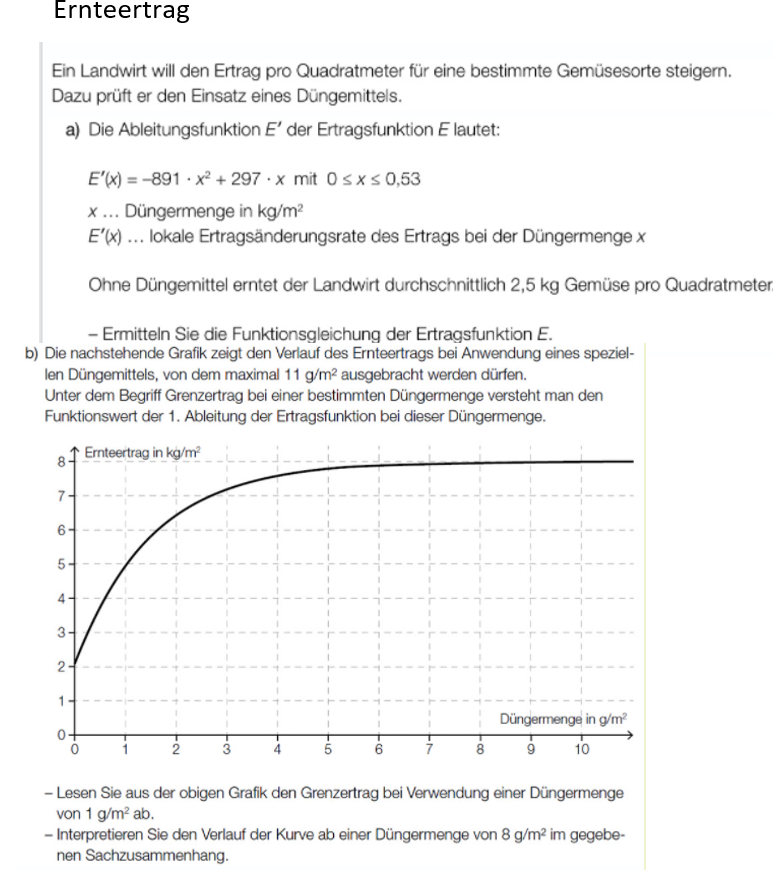
b) Die nachstehende Grafik zeigt den Verlauf des Ernteertrags bei Anwendung eines speziellen Düngemittels, von dem maximal \( 11 \mathrm{~g} / \mathrm{m}^{2} \) ausgebracht werden dürfen. Unter dem Begriff Grenzertrag bei einer bestimmten Düngermenge versteht man den Funktionswert der 1. Ableitung der Ertragsfunktion bei dieser Düngermenge.
- Lesen Sie aus der obigen Grafik den Grenzertrag bei Verwendung einer Düngermenge von \( 1 \mathrm{~g} / \mathrm{m}^{2} \) ab.
- Interpretieren Sie den Verlauf der Kurve ab einer Düngermenge von \( 8 \mathrm{~g} / \mathrm{m}^{2} \) im gegebenen Sachzusammenhang.