Aufgabe:
Gegeben sind die Funktionen f und h mit den Funktionsgleichungen:
f(x) = (x-3) * e^x
h(x) = x-3
Bestimmen Sie rechnerisch die beiden Schnittstellen der Graphen der Funktionen f und h .
[Zur Kontrolle: Die Schnittstellen sind x = 0 und x = 3.]
Problem/Ansatz:
Dies ist eine Aufgabe aus der Abiprüfung 2022 Mathe LK NRW (hilfsmittelfreier Teil).
In der Lösung ist folgendes geschrieben: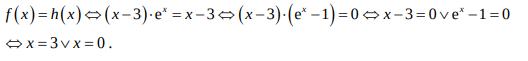
Text erkannt:
\( \begin{array}{l}f(x)=h(x) \Leftrightarrow(x-3) \cdot \mathrm{e}^{x}=x-3 \Leftrightarrow(x-3) \cdot\left(\mathrm{e}^{x}-1\right)=0 \Leftrightarrow x-3=0 \vee \mathrm{e}^{x}-1=0 \\ \Leftrightarrow x=3 \vee x=0 .\end{array} \)
Wie kommen die von (x-3) * e^x = x-3 zu (x-3) * (e^x - 1) = 0 ?