Vom Duplikat:
Titel: Stellen Sie den Sachverhalt in der Vierfeldertafel dar
Stichworte: vierfeldertafel
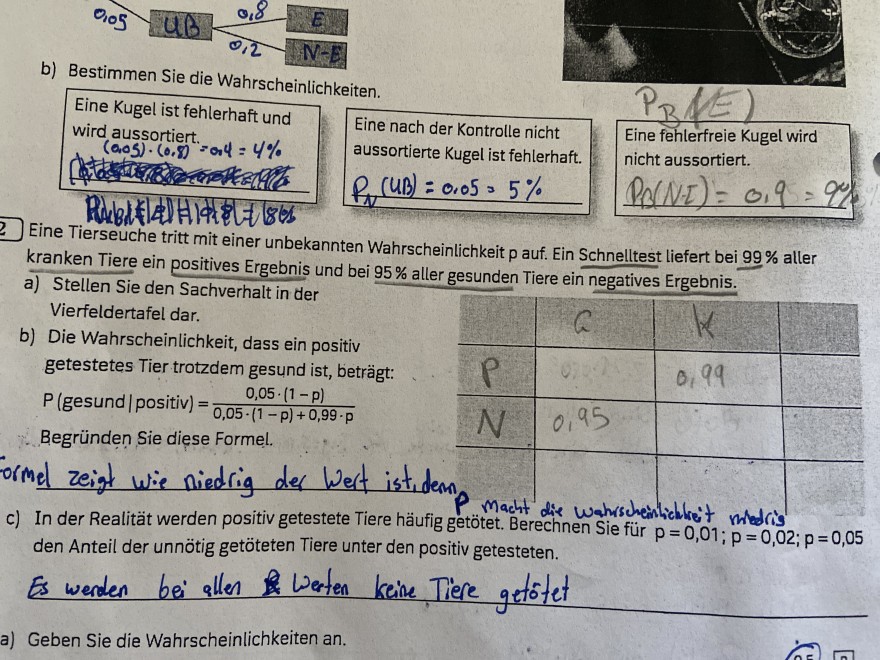

Text erkannt:
Eine Tierseuche tritt mit einer unbekannten Wahrscheinlichkeit p auf. Ein Schnelltest liefert bei \( 99 \% \) aller kranken Tiere ein positives Ergebnis und bei \( 95 \% \) aller gesunden Tiere ein negatives Ergebnis.
a) Stellen Sie den Sachverhalt in der Vierfeldertafel dar.
b) Die Wahrscheinlichkeit, dass ein positiv getestetes Tier trotzdem gesund ist, beträgt:
\( P \) (gesund | positiv) \( =\frac{0,05 \cdot(1-p)}{0,05 \cdot(1-p)+0,99 \cdot p} \) Begründen Sie diese Formel.
c) In der Realität werden positiv getestete Tiere häufig getötet. Berechnen Sie für \( p=0,01 ; p=0,02 ; p=0,05 \) den Anteil der unnötig getöteten Tiere unter den positiv getesteten.
Aufgabe:
Wie kann ich die Zahlen in der vierfeldertafel legen?
Kann man mir helfen ?
Danke
Problem/Ansatz: