Das MIT, das Dreieck und die Eintrittsprüfung

Question

Aufgabe:

Heute verbreitete der Newsletter IFLScience eine Aufgabe, angeblich eine Eintrittsprüfung des MIT aus dem vorletzten Jahrhundert. Es wird nach der Länge von x gefragt:

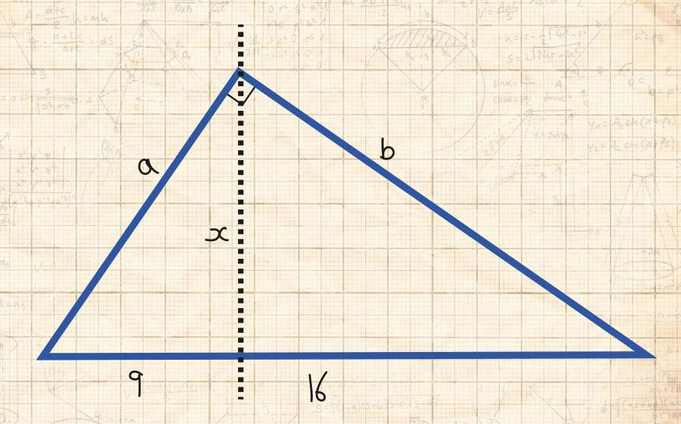
Und tatsächlich, ich bin fündig geworden, die Aufgabe kommt wirklich vom MIT. Das Urheberrecht dürfte abgelaufen sein, deswegen erlaube ich mir, sie hier zu reproduzieren:

Answer 1

Es handelt sich um das kleinste pythagoreische Dreieck, dass in zwei pythagoreische Dreiecke zerlegt werden kann. Ohne elektronisches Werkzeug und dem Wissen des 3,4,5-Dreiecks ist sie leichter lösbar als mit elektronischem Werkzeug. Es genügt allerdings auch die Kenntnis des Höhensatzes.

Comments

Ich bin ziemlich zuversichtlich, dass es 1869 keine elektronischen Werkzeuge gab :)

---

Diese Zuversicht teile ich.

Answer 2

Aloha :)

Pythagoras liefert direkt aus der Abbildung:$$a^2=9^2+x^2\quad;\quad b^2=16^2+x^2\quad;\quad a^2+b^2=(9+16)^2\quad\implies$$$$(9^2+x^2)+(16^2+x^2)=a^2+b^2=(9+16)^2=9^2+16^2+2\cdot9\cdot16\quad\implies$$$$2x^2=2\cdot9\cdot16\quad\implies\quad x^2=9\cdot16=3^2\cdot4^2=(3\cdot4)^2\quad\implies\quad x=12$$

Interessant, dass man 1869 mit dem Wissen aus der 7-ten Klasse ans MIT konnte ;)

Comments

Ich sehe gerade, dieses Problem wurde vor 5 Jahren schon mal ausgegraben: