Bestimmen Sie die 1., 2. und 3. Ableitung der Funktion f.

Question

Aufgabe:

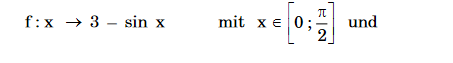
Text erkannt:

\( \mathrm{f}: \mathrm{x} \rightarrow 3-\sin \mathrm{x} \quad \) mit \( \mathrm{x} \in\left[0 ; \frac{\pi}{2}\right] \) und

Bestimmen Sie die 1., 2. und 3. Ableitung der Funktion f.

Problem/Ansatz:

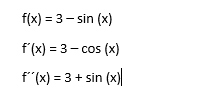
Text erkannt:

\( f(x)=3-\sin (x) \)
\( f^{\prime}(x)=3-\cos (x) \)
\( f^{\prime \prime}(x)=3+\sin (x) \)

Ist damit das ableiten gemeint? Verstehe die Fragestellung nicht ganz

Answer 1

f ( x ) = 3 - sin(x)
f´( x ) = - cos(x)
f ´´ ( x ) = sin(x)
f´´´(x) = cos(x)

Die 3 entfällt beim ableiten

Comments

Entschuldigen Sie, aber könnten sie nochmal drüberschauen, ob ich diese teilaufgabe jetzt richtig abgeleitet habe.

Text erkannt:

\( \mathrm{g}: \mathrm{x} \rightarrow 4 \cos \mathrm{x}+2 \mathrm{x} \quad \) mit \( \mathrm{x} \in\left[0 ; \frac{\pi}{2}\right] \)

Text erkannt:

\( g(x)=4 \cos (x+2 x) \)
\( g^{\prime}(x)=-4 \sin (3 x)^{*} 3 \)
\( g^{\prime}(x)=-12 \sin (3 x) \)
\( g^{\prime \prime}(x)=-12-\cos (3 x) \)
\( g^{\prime \prime \prime}(x)=-12 \sin (3 x) \)

---

Du hast falsch geklammert
g ( x ) = 4 * cos ( x ) + 2 * x
g´ ( x ) = - 4 * sin ( x ) + 2
g´´ ( x ) = - 4  *  cos ( x )
g´´´ ( x ) = 4 * sin ( x )

Zum Dank wirst du bis MItermacht einhalten :

Ich will Vater und Mutter ehren als ob sie
meine Eltern wären.