Aufgabe:
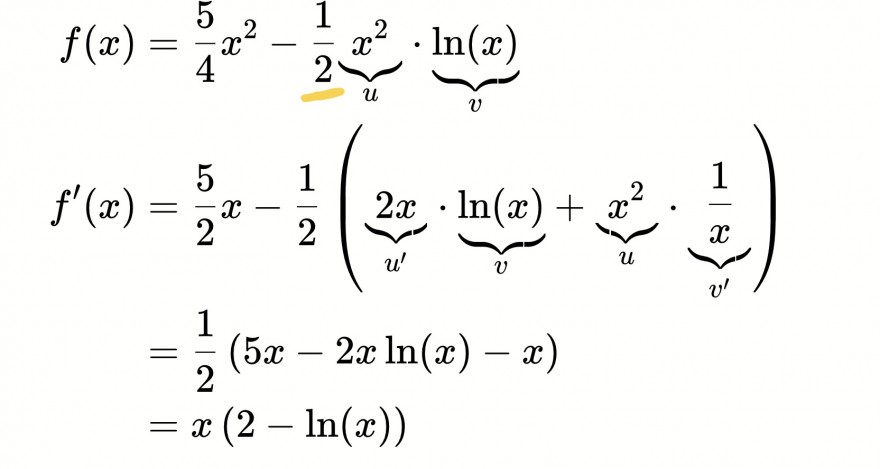
Text erkannt:
\( \begin{aligned} f(x) &=\frac{5}{4} x^{2}-\frac{1}{2} \underbrace{x^{2}}_{u} \cdot \underbrace{\ln (x)}_{v} \\ f^{\prime}(x) &=\frac{5}{2} x-\frac{1}{2}(\underbrace{2 x}_{u^{\prime}} \cdot \underbrace{\ln (x)}_{v}+\underbrace{x^{2}}_{u} \cdot \underbrace{\frac{1}{x}}_{v^{\prime}}) \\ &=\frac{1}{2}(5 x-2 x \ln (x)-x) \\ &=x(2-\ln (x)) \end{aligned} \)
Warum gehört dieser Faktor nicht zu „u“?
Problem/Ansatz:
Warum gehört dieser Faktor nicht mit zu „u“? Würde er dazugehören, wenn der erste Summand nicht wäre?
Vielen Dank