Auch wenn nun minus dazwischen steht, stimmen die beiden angeführten Ableitungen.
Du kannst nun einfach so zusammenfassen:
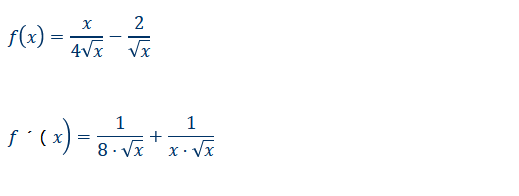
Text erkannt:
\( f(x)=\frac{x}{4 \sqrt{x}}-\frac{2}{\sqrt{x}} \)
\( f^{\prime}(x)=\frac{1}{8 \cdot \sqrt{x}}+\frac{1}{x \cdot \sqrt{x}} \)