Bestimmen Sie die Funktionsgleichung einer ganzrationalen Funktion 3.

Question

Text erkannt:

\( \underline{\text { Aufgabe } 1} \)
a) Bestimmen Sie die Funktionsgleichung einer ganzrationalen Funktion 3. Grades, deren Graph durch den Ursprung geht, im Punkt \( \mathrm{P}\left(2 ; \mathrm{f}_{(2)}\right) \) einen Sattelpunkt und an der Stelle \( \mathrm{x}=-2 \) die Steigung 6 besitzt.
b) Formel 1-Strecken haben häufig bei Start und Ziel zwei Geraden, die parallel verlaufen (siehe Skizze):
1. die eigentliche Rennstrecke (unten)
und
2. die Boxengasse, in der die Fahrzeuge aufgetankt werden.
Der Übergang von der im Diagramm oben dargestellten Boxengasse zu der unteren Rennstrecke soll durch den Graphen einer Polynomfunktion beschrieben werden.
Bestimmen Sie eine Funktion \( 3 . \) bzw. 5. Grades, die einen knickund ruckreien Übergang in den Punkten \( \mathrm{P}_{1}(-5 ;-5) \) und \( \mathrm{P}_{2}(5 ; 5) \)
gewährleistet.

Aufgabe:

Answer 1

Benutze http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm zur Hilfe und Selbstkontrolle

Eigenschaften

f(0)=0
f'(2)=0
f''(2)=0
f'(-2)=6

Gleichungssystem

d = 0
12a + 4b + c = 0
12a + 2b = 0
12a - 4b + c = 6

Errechnete Funktion und Ableitung(en)

f(x) = 0,125·x^3 - 0,75·x^2 + 1,5·x
f'(x) = 0,375·x² - 1,5·x + 1,5
f''(x) = 0,75·x - 1,5
f'''(x) = 0,75

Answer 2

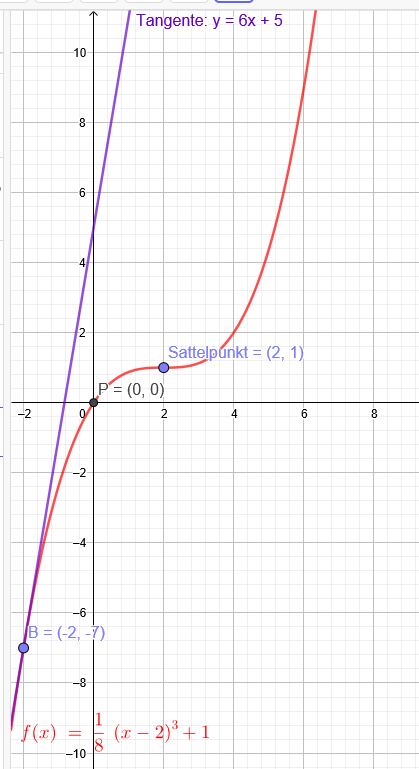
a) Ich verschiebe den Graph so, dass der Sattelpunkt auf der x-Achse liegt:(Dreifachnullstelle)

p(x)=a*(x-2)^3

p´(x)=3a*(x-2)^2

p´(-2)=3a*(-2-2)^2 =48a

48a=6

a=\( \frac{1}{8} \)

p(x)=\( \frac{1}{8} \)*(x-2)^3

f(x)=\( \frac{1}{8} \)*(x-2)^3+c

P(0|0)

f(0)=\( \frac{1}{8} \)*(0-2)^3+c=-1+c

-1+c=0

c=1

f(x)=\( \frac{1}{8} \)*(x-2)^3+1