e^e als obergrenze fürs integral? Integrale berechnen

Question

HII LEUTE!!

Das Wetter ist perfekt. Was nicht perfekt ist, ist meine Laune.

Ich soll das folgende Integral berechnen:

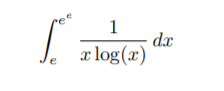
Text erkannt:

\( \int \limits_{e}^{e^{e}} \frac{1}{x \log (x)} d x \)

e^e als obergrenze fürs integral? HALLO?

log(x) im nenner? HALLO? Leute... ich kann das nicht und brauche mal hilfe.

Kann mir jemand bitte nen rechenweg geben? Würde eure Augen knutschen.

LG euer Matheloosa

Answer 1

Aloha :)

Das ist ein Standard-Integral der Form:$$\int\frac{f'(x)}{f(x)}\,dx=\ln\left|f(x)\right|+\text{const}$$Daher kannst du sofort hinschreiben:$$\int\limits_e^{e^e}\frac{1}{x\ln x}dx=\int\limits_e^{e^e}\frac{1/x}{\ln x}dx=\left[\ln\left|\ln x\right|\right]_e^{e^e}=\ln(\underbrace{\ln(e^e)}_{e\ln(e)=e})-\overbrace{\ln(\underbrace{\ln(e)}_{=1})}^{=0}=\ln(e)=1$$

Comments

ich liebe dich und ich meins ernst.

Answer 2

 \( \int \limits_{e}^{e^{e}} \frac{1}{x \cdot \ln (x)} \cdot d x \)
\( \int \frac{1}{x \cdot \ln (x)} \cdot d x \)
Substitution:
\( u=\ln x \)
\( \frac{d u}{d x}=\frac{1}{x} \)
\( d x=x \cdot d u \)
\( \int \frac{1}{x \cdot u} \cdot x \cdot d u=\int \frac{1}{u} \cdot d u=\ln (u) \)
Resubstitution:
\( \int \limits_{e}^{e^{e}} \frac{1}{x \cdot \ln (x)} \cdot d x=\left[\ln (\ln (x)]_{e}^{e^{e}}=\left[\ln \left(\ln \left(e^{e}\right)\right]-[\ln (\ln (e)]=[\ln (e \cdot \ln (e)]-0=\right.\right. \)
\( =[\ln (e \cdot 1]-0=1 \)

Answer 3

Hallo,

die Ableitung von \(\ln(x)\) ist \(\frac{1}{x}\). Das kann man hervorragend ausnutzen. Substitutiere hierzu \(u:=\ln(x)\), dann gilt \(\frac{\mathrm{d}u}{\mathrm{d}x}=\frac{1}{x}\Rightarrow \mathrm{d}x=x\mathrm{d}u\). Also:$$\int \limits_{e}^{e^e}\frac{1}{x\ln(x)}\,\mathrm{d}x=\int \limits_{\ln(e)}^{\ln(e^e)}\frac{1}{\cancel{x}u}\cancel{x}\, \mathrm{d}u=\int \limits_{1}^{e}\frac{1}{u}\, \mathrm{d}u=\left.\ln(u)\right|_{1}^{e}=\ln(e)-\ln(1)=1$$

Answer 4

Hallo,

unter der Annahme, das log(x) = ln(x) ist:

Substituiere z= ln(x)

dz/dx= 1/x

dx=x dz

in den Integranden eingesetzt und x gekürzt:

=∫1/z dz =ln|z|+C

die Grenzen substituiert:

z=ln(x) =ln(e^e)= e ln(e)= e (obere Gr.)

z=ln(x)=ln(e) =1 untere Grenze

-------->

=ln|e| -ln|1| = 1-0=1

hilfreich auch:

https://www.integralrechner.de/

sowas hatte ich früher nicht :)