Aufgabe:

Text erkannt:
Beweisen Sie, dass die folgenden Codes linear sind. LösUNGSTIPP
Sie können entweder:
- zeigen, dass alle Summen der Form \( w_{i}+w_{j} \) wieder in \( C \) sind,
- eine Generatormatrix für \( C \) finden oder
- eine Prüfmatrix für \( C \) finden.
1.) \( C_{1}=\{00000,10101,01010,11111\} \)
2.) \( C_{2}=\{00000,00100,01010,01110,10001,10101,11011,11111\} \)
3.) \( C_{3}=\{00000,00101,01000,01101,10010,10111,11010,11111\} \)
Lösung zu der Aufgabe
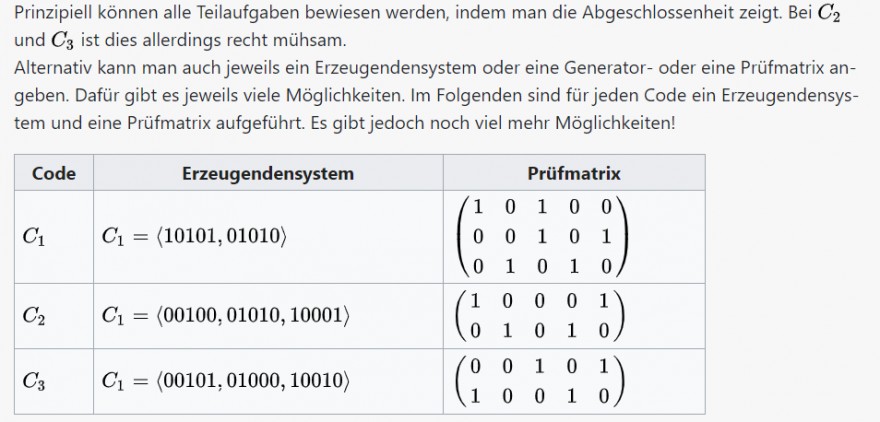
Text erkannt:
Prinzipiell können alle Teilaufgaben bewiesen werden, indem man die Abgeschlossenheit zeigt. Bei \( C_{2} \) und \( C_{3} \) ist dies allerdings recht mühsam. Alternativ kann man auch jeweils ein Erzeugendensystem oder eine Generator- oder eine Prüfmatrix angeben. Dafür gibt es jeweils viele Möglichkeiten. Im Folgenden sind für jeden Code ein Erzeugendensystem und eine Prüfmatrix aufgeführt. Es gibt jedoch noch viel mehr Möglichkeiten!
\begin{tabular}{|l|l|l|l|}
\hline Code & \multicolumn{1}{|c|} { Erzeugendensystem } & \multicolumn{6}{|c|} { Prüfmatrix } \\
\hline\( C_{1} \) & \( C_{1}=\langle 10101,01010\rangle \) & \( \left(\begin{array}{lllll}1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0\end{array}\right) \) \\
\hline\( C_{2} \) & \( C_{1}=\langle 00100,01010,10001\rangle \) & \( \left(\begin{array}{lllll}1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0\end{array}\right) \) \\
\hline\( C_{3} \) & \( C_{1}=\langle 00101,01000,10010\rangle \) & \( \left(\begin{array}{lllll}0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0\end{array}\right) \) \\
\hline
\end{tabular}
Problem/Ansatz:
Kann mir bitte jemand ausführlich erklären, wie man von einem gegeben linearen Code eine Generatormatrix und eine Prüfmatrix erstellt. Also ich habe mir es versucht mit der Lösung herzuleiten. Aber ich habe es nicht verstanden.
Das mit dem Erzeugendensystem habe ich verstande. Nur desto größer der Code, desto umständlicher wird diese vorgehensweise.
Deswegen würde ich auch gerne das Prinzip der Prüf und Generatormatrix verstehen.
Vielen Dank für Eure Hilfe im Voraus