Die Sinusfunktion approximieren an der kleinsten positiven Minimalstelle.

Question

Ich soll den Sinus mit folgender Herangehensweise approximieren: Ermitteln sie diejenige parabel die sich in der kleinsten positiven minimalstelle des sinus am besten an den graphen der funktion f(x)=sin(x) , R-->R , anpasst.

Ich weiß nicht wie ich an die aufgabe herangehen soll.

Answer 1

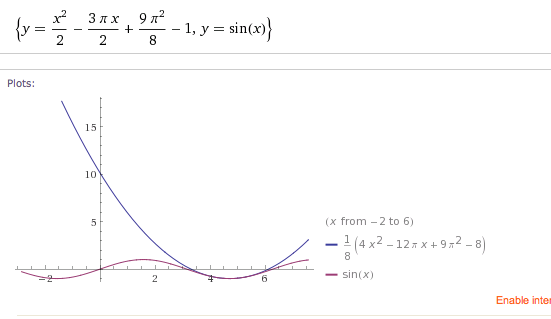
Als erstes musst du wissen, was die kleinste positive Minimalstelle des Sinus ist. Ich tippe da auf x= 270°=3π/2.

Daher hat die Parabel den Scheitelpunkt in S(3π/2 , -1).

Nun Ansatz:

y = a(x - 3π/2)^2 - 1

Vergleich mit y=sin(x). Wir haben schon dafür gesorgt, dass beide Kurven in S(3π/3, -1) eine Extremalstelle haben.
Nun sollten noch die beiden Krümmungen gleich sein.

Daher y=sin(x) und y= a(x - 3π/2)^2 - 1 zwei mal ableiten.

y'=cos(x), y'' = -sin(x), 3π/2 einsetzen    y'' = 1

y= a(x - 3π/2)^2 - 1

y' = 2a(x-3π/2)*1 = 2ax - 3π

y'' = 2a

Krümmungen gleichsetzen

2a = 1

a= 1/2

y = 1/2(x-3π/2)^2 - 1 = 1/2 ( x^2 -3πx + 9π^2/4) - 1

= 1/2 x^2 -3π/2 x + 9π^2 /8 -1

Skizze erstellt mit https://www.wolframalpha.com/input/?i=y%3D+1%2F2+x%5E2+-3π%2F2+x+%2B+9π%5E2+%2F8+-1+%2C+y%3Dsinx

Comments

Danke.

Eine frage hätte ich aber noch. Ist es wirklich in ordnung dass ich die zweite ableitung für die krümmung verwende? Ich dachte mit hilfe der zweiten ableitung kann ich nur ermitteln ob es sich um eine links oder rechtskrümmung handelt.