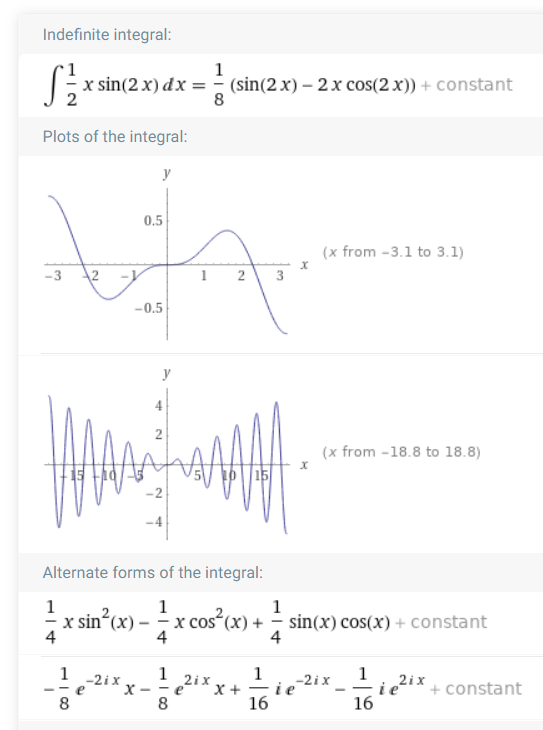
Ich empfehle meist wenn einem die eigenen Ideen ausgehen z.B Wolframalpha zu fragen
Bei den alternativen Formen wird man dann schnell fündig.
Natürlich darf man sich dann gerne Fragen warum das gilt. Aber vermutlich ahnt man dann schon das die Vereinfachung über die Additionstheoreme läuft.
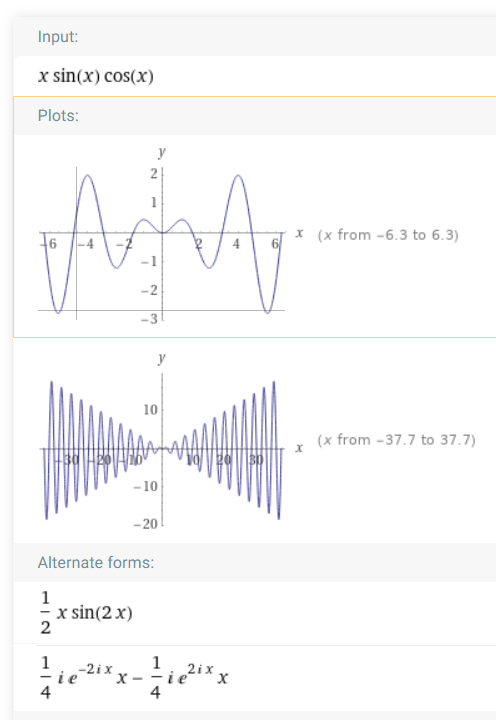
Und dann kann man sich noch eine Anregung für das unbestimmte Integral holen.