\( \frac{2-x}{-2 x}+1<-2 \)
\( \frac{2-x}{-2 x}<-3 \)|*(-1)
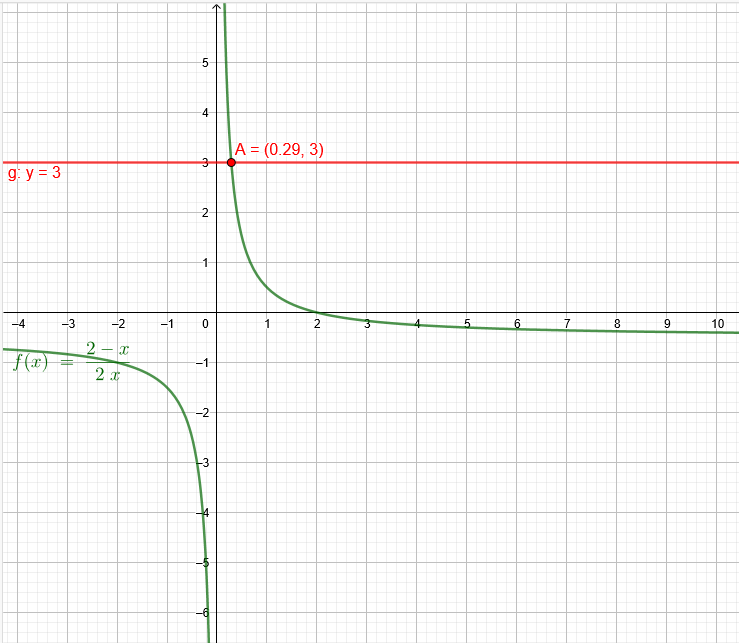
\( \frac{2-x}{2 x}>3 \)
1.Fall : x>0
2-x>6x → 2>7x →x<\( \frac{2}{7} \)
2.Fall : x=0 → f(x) hat dort einen Pol
3.Fall : x<0
z.B: x=-1
\( \frac{2+1}{2 }>3 \) geht nicht
Lösungsmenge: 0<x<\( \frac{2}{7} \)