Wachstumsfunktion Bakterien mit Basis e

Question

22. Eine Bakterienkultur wird um 9 Uhr sich selbst überlassen. Ihr Wachstum wird durch die Gleichung b(t) = 4000 e 0,5 t beschrieben, wobei b(t) die Anzahl der Bakterien ist und die Zeiteinheit von t Stunden (h) ist. a) Wie viele Bakterien sind um 9 Uhr vorhanden? b) Wie viele Bakterien sind es um 13 Uhr 30? c) Zu welchem Zeitpunkt hat sich der Bestand verdoppelt? d) Wie viele Bakterien entstehen in der 3. Stunde? e) Um wie viel Prozent wächst die Bakterienkultur pro Stunde? f) Zeigen Sie b '(t) = 0,5 b (t) Welche Bedeutung hat diese Gleichung?


Bitte mit ausführlichen Rechenschritte ! Auch wenn man das e aufhebt mit In

Answer 1

Hallo rennu,

 

ich vermute, die Funktionsgleichung soll sein:

b(t) = 4000 * e^0,5t

 

a) Wie viele Bakterien sind um 9 Uhr vorhanden?

Um 9 Uhr gilt t = 0, also

b(0) = 4000 * e^0,5*0 = 4000 * e⁰ = 4000 * 1 = 4000

 

b) Wie viele Bakterien sind es um 13 Uhr 30?

13:30 Uhr entspricht t = 4,5

b(4,5) = 4000 * e^{0,5 * 4,5} = 4000 * e^2,25 ≈ 37951

Kaum vorstellbar, aber der Graph sieht tatsächlich so aus:

 

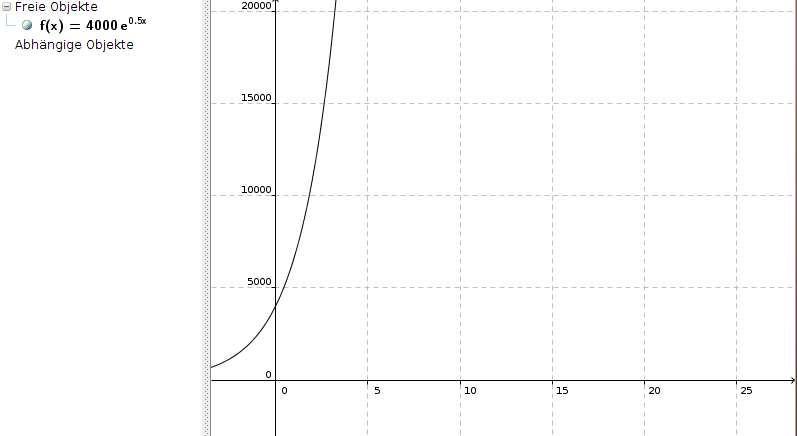
c) Zu welchem Zeitpunkt hat sich der Bestand verdoppelt?

b(t) = 4000 * e^0,5t = 8000 | :4000

e^0,5t = 2

Nun wird auf beiden Seiten der natürliche Logarithmus gezogen; bei e nimmt man einfach den Exponenten, weil ln die Umkehrfunktion von e ist:

0,5t = ln(2)

t = 2 * ln(2) ≈ 1,39

Nach ca. 1,39 Stunden hat sich die Bakterienkultur verdoppelt. 1/100 einer Stunde = 36 Sekunden, demnach sind 39/100 einer Stunde 39 * 36 Sekunden = 1404 Sekunden = 23 Minuten und 24 Sekunden.

Also hat sich die Bakterienkultur um ca. 10:23:24 Uhr verdoppelt.

Probe:

b(1,39) = 4000 * e^1,39/2 = 4000 * e^0,695 ≈ 8014,83

(Rundungsfehler)

 

Das muss jetzt erst einmal reichen :-)

 

Besten Gruß

Comments

Vielen vielen Dank , die ersten hätte ich noch selbst hinbekommen. Außer die letzten zwei. :(


d) In die Zeit setzt man ja einfach die drei ein.


e) muss ich k wieder berechnen?

---

Gern geschehen :-D

 

d) Wie viele Bakterien entstehen in der 3. Stunde?

"In die Zeit setzt man ja einfach die drei ein."

 

Nö, ganz so einfach ist es nicht: Wenn wir wissen wollen, wie viele Bakterien in der 3. Stunde entstehen, müssen wir die Anzahl der Bakterien am Ende der 2. Stunde von der Anzahl der Bakterien am Ende der 3. Stunde subtrahieren. Logisch? Hätten wir am Ende der 3. Stunde zum Beispiel 50000 Bakterien und am Ende der 2. Stunde 30000 Bakterien, wären in der 3. Stunde 50000 - 30000 = 20000 Bakterien entstanden.

Jetzt mit den konkreten Zahlen der gegebenen Funktionsgleichung:

b(3) - b(2) =

4000 * e^1,5 - 4000 * e¹ ≈ 7054

 

Rest folgt :-)

---

oh nein, dies bringt mich aus dem Konzept .....meine Logik war halt ziemlich knapp und bündig :D


I am waiting for the last :)

---

e) Um wie viel Prozent wächst die Bakterienkultur pro Stunde?

"muss ich k wieder berechnen?"

 

Welches k?

Nein, Du gehst einfach so vor:

 

Nach n Stunden (n ∈ ℕ) haben wir b(n) Bakterien.

Eine Stunde später haben wir b(n+1) Bakterien.

Um das Verhältnis bzw. den Wachstumsfaktor heraus zu bekommen, rechnen wir

b(n+1)/b(n), also

(4000 * e^{0,5 * (n+1)}) / (4000 * e^{0,5 * n})

Die 4000 werden weggekürzt, es bleibt

e^{0,5 * (n+1)} / e^{0,5 * n} =

e^{0,5 * (n+1) - 0,5 * n} =

e^{0,5n + 0,5 - 0,5n} =

e^0,5 ≈ 1,6487

Die Bakterienkultur wächst also pro Stunde um ca. 64,87%

 

Rest folgt :-)

---

f) Zeigen Sie b '(t) = 0,5 b (t) Welche Bedeutung hat diese Gleichung?

 

b(t) = 4000 * e^0,5t

Der Faktor 4000 bleibt bei der Ableitung bestehen. Die Ableitung von e^0,5t wird berechnet durch

Äußere Ableitung * Innere Ableitung

Äußere Ableitung = e^0,5t

Innere Ableitung = (0,5t)' = 0,5

Insgesamt:

b'(t) = 4000 * 0,5 * e^0,5t = 2000 * e^0,5t = 0,5 * b^t

 

Die 1. Ableitung b'(t) gibt die Steigung (oder Veränderung) der Funktion b(t) an der Stelle t an.

Wie Du der Graphik in meiner ursprünglichen Antwort entnehmen kannst, wächst die Anzahl der Bakterien im Laufe der Zeit immer stärker an (z.B. ist das Wachstum in der 1. Stunde kleiner als das Wachstum in der 3. Stunde).

Genau dies wird durch die 1. Ableitung ausgedrückt :-)

 

Besten Gruß

---

sry, eine ganz kleine frage

 

die 4000 wird gekürzt

 

und dann folgt ja dies in der klammer mit n+1 und so

 

bitte etwas ausführlich wie dies berechnet wird

 

e^{0,5 * (n+1)} / e^{0,5 * n} =

e^{0,5 * (n+1) - 0,5 * n} =

 

danke im voraus

---

Hallo rennu,

 

wenn Du zwei Zahlen mit gemeinsamer Basis, aber unterschiedlichen Exponenten durcheinander dividierst, subtrahierst Du einfach die Exponenten, zum Beispiel

 

2⁵/2³ = 2^5-3 = 2² = 4

Probe:

32/8 = 4

 

5⁴/5² = 5^4-2 = 5² = 25

Probe:

625/25 = 25

 

7⁶/7⁴ = 7^6-4 = 7² = 49

Probe:

117649/2401 = 49

 

Allgemein:

a^x/a^y = a^x-y

 

In unserer Aufgabe hatten wir aber nicht 2, 5 oder 7 als Basis, sondern e ≈ 2,7182818285

Das Vorgehen blieb dasselbe.

0,5 * (n+1) - 0,5 * n

auszurechnen bereitet Dir dann sicherlich keine Schwierigkeiten!

---

natürlich bereitet es mir schwierigkeiten ;'(


0,5 * (n+1) - 0,5 * n  wo ist das e hingeblieben ..........


muss ich jetzt ausmultiplizieren und zusammenfassen.....ja, ich weiß, mit mir ist es wie eine schwere geburt.......deshalb hat  gorgor sich nicht mehr blicken lassen ;D sonst ist er derjenige der mir hilft :)

---

Na, ich bitte Dich :-)

0,5 * (n + 1) - 0,5 * n | Klammer ausmultiplizieren

0,5 * n + 0,5 * 1 - 0,5 * n | Umstellen

0,5 * n - 0,5 * n + 0,5 * 1 | Die Differenz der ersten beiden Produkte ergibt 0:

0 + 0,5 * 1

0,5 * 1

0,5

---

oh gott , echt nett ! :) Danke !!!!!!

---

Sehr gern geschehen :-)

Bei Rückfragen zögere nicht, Dich nochmals zu melden!!

P.S. Danke für den Stern :-D