Ich habe folgende Gleichungen:
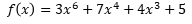
Text erkannt:
\( f(x)=3 x^{6}+7 x^{4}+4 x^{3}+5 \)
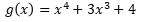
Text erkannt:
\( g(x)=x^{4}+3 x^{3}+4 \)
Es sollen zwei Polynome q und r gesucht werden mit
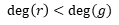
Text erkannt:
\( \operatorname{deg}(r)<\operatorname{deg}(g) \)
sodass:
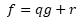
Text erkannt:
\( f=q g+r \)
gilt.
Dies sollen wir suchen in folgenden Polynomringen
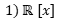
Text erkannt:
1) \( \mathbb{R}[x] \)

Text erkannt:
2) \( \mathbb{Z}_{11}[x] \)
Problem/Ansatz:
Ich weiß soweit, dass ich das mit einer Polynomdivision lösen soll aber es weicht von der Lösung ab. Wäre für einen Rechenweg für diese Aufgabe dankbar.
und wie ist das mit dem deg() gemeint und dem f = qg+r ?
Ist damit gemeint r soll einen geringeren Grad als g haben, also kleiner x^4 ?
Das soll bei der 1) rauskommen, bei der 2) hab ich keine Lösung
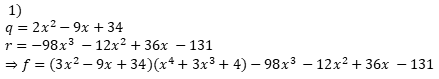
Text erkannt:
1) \( q=2 x^{2}-9 x+34 \)
\( r=-98 x^{3}-12 x^{2}+36 x-131 \)
\( \Rightarrow f=\left(3 x^{2}-9 x+34\right)\left(x^{4}+3 x^{3}+4\right)-98 x^{3}-12 x^{2}+36 x-131 \)
Wäre für eine Hilfestellung dankbar.
VG coffee.cup