Wie löse ich folgende Ungleichung?

Question

Aufgabe:

Wie löse ich folgende Ungleichung?

$$\sqrt{|x+2|} \leq |x+1|$$

Ich habe länger rumprobiert, kam jedoch nie auf das ganz richtige Ergebnis. Weiß da jemand weiter?

Danke für die Hilfe.

Comments

Quadriere beide Seiten, Betragsstriche kann man weglassen, weil beide Seiten

nicht negativ werden können.

-> x+2 <= x^2+2x+1

x^2+x-1 <= 0

pq-Formel:

....

---

Für alle reellen x

Answer 1

Hallo,

graphisch sieht das so aus:

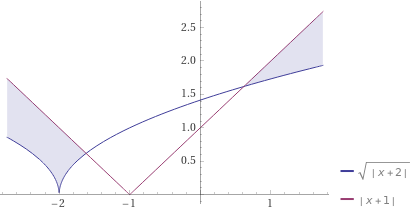
\(\sqrt{|x+2|} \leq |x+1|\)

|x+2|≤|x+1|²

x+2≤x²+2x+1   *)

0≤x²+x-1

Bei Gleichheit:

0=x²+x-1

x=-0,5±√1,25

x≈-1.618 oder x≈0.618

Da y=x²+x-1 eine nach oben geöffnete verschobene Normalparabel beschreibt, ist die Ungleichung 0≤x²+x-1 erfüllt für

x≤-1.618 oder x≥0.618

:-)

*)

PS:

-x-2≤x²+2x+1

0≤x²+3x+3

x=+1.5±√(2.25-3) → Keine reelle Lösung!

Comments

Danke für die Hilfe.

Eine Sache ist mir jedoch unklar. Und zwar soll man die Ungleichung für alle reellen x lösen. Demnach kann man doch auf der linken Seite der Ungleichung für |x+2| die Betragsstriche nach dem Quadrieren nicht einfach weglassen.

VG

---

Hallo Chris,

du hast ja recht. Ich habe meine Antwort ergänzt. Demnach gibt es keine weiteren reellen Lösungen.

:-)