Hallo Leute,
Hier ist meine Aufgabe
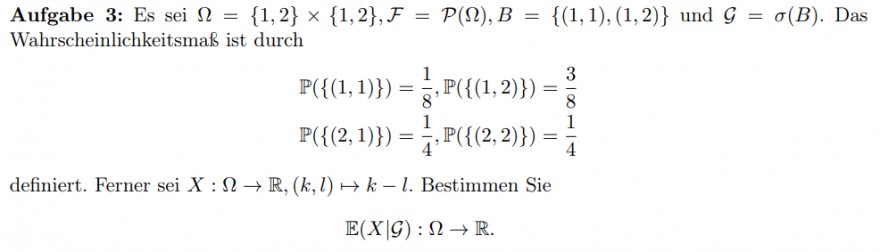
Text erkannt:
Aufgabe 3: Es sei \( \Omega=\{1,2\} \times\{1,2\}, \mathcal{F}=\mathcal{P}(\Omega), B=\{(1,1),(1,2)\} \) und \( \mathcal{G}=\sigma(B) . \) Das
Wahrscheinlichkeitsmaß ist durch
$$ \begin{array}{l} \mathbb{P}(\{(1,1)\})=\frac{1}{8}, \mathbb{P}(\{(1,2)\})=\frac{3}{8} \\ \mathbb{P}(\{(2,1)\})=\frac{1}{4}, \mathbb{P}(\{(2,2)\})=\frac{1}{4} \end{array} $$
definiert. Ferner sei \( X: \Omega \rightarrow \mathbb{R},(k, l) \mapsto k-l \). Bestimmen Sie
$$ \mathbb{E}(X \mid \mathcal{G}): \Omega \rightarrow \mathbb{R} $$
und meine Lösung ist:

Text erkannt:
X ist messbar, also konstant \( =\alpha \) auf \( \mathrm{B} \) und konstant \( =\beta \) auf \( \mathrm{B}^{\mathrm{c}} \) \( \alpha: E\left(1_{B} Y\right)=E\left(1_{B} X\right) \)
\( \beta: E\left(1_{B^{c}} y^{y}\right)=E\left(1_{B^{c}} X\right] \)
Es gilt:
\( E\left(1_{B} Y\right)=\alpha \cdot P(B)=\alpha \cdot\left(\frac{3}{8}+\frac{3}{8}\right)=\alpha \cdot\left(\frac{3}{4}\right) \)
\( E\left(1_{B} x\right)=(1-1) \cdot \frac{3}{8}+(1-2) \cdot \frac{3}{8}=-\frac{3}{8} \)
Jetzt ist leider die Erwartungswert kleiener als \( 0 . \)
Kann ich noch weiter machen?
Also \( \alpha \cdot \frac{3}{4}=-\frac{3}{8} \rightarrow \alpha=-\frac{1}{2} \)
\( E(X G)(w)=\frac{E\left(1_{B} x\right)}{P(B)}=\frac{ \left.\left((1-1) \cdot \frac{3}{8}+(1-2) \cdot \frac{3}{8}\right)\right)}{\frac{3}{8}+\frac{3}{8}}=-\frac{1}{2} \)
Ist es doch richtig? Oder kann der Erwartungswert nicht kleiner als 0 sein?
Liebe Grüße
Thomas