Reihen auf Konvergenz best.

Question

Aufgabe:

Untersuchen Sie die folgenden Reihen auf Konvergenz:

$\sum\limits_{n=0}^{\infty}{(-1)^n \frac{n}{3^n}}$ und $\sum\limits_{n=1}^{\infty}{\frac{1}{\sqrt{n}}}$

Problem/Ansatz:

Für die erste Reihe hätte ich diese Lösung:

| $\frac{\frac{n+1}{3^n+1}}{\frac{n}{3^n}}$ |

= $\frac{1}{3}$ * $\frac{n+1}{n}$ -> $\frac{1}{3}$ < 1

Wäre das so richtig, oder gibt es eine bessere Lösung?

Zur zweiten weiß ich nicht wie man das mit Brüchen macht. Wie muss man da vorgehen?

Answer 1

Moin vovi,

deine Lösung für die erste Reihe ist korrekt. Alternativ könntest du noch das Leibniz-Kriterium verwenden, denn es gilt

$\frac{n}{3^n} > \frac{n+1}{3^{n+1}}$ für alle $n \in \mathbb{N}_{\geq 1}$, womit $\frac{n}{3^n}$ eine monoton fallende Folge ist. Das Leibniz-Kriterium liefert dir dann die Kovnergenz.

Bei deiner zweiten Reihe kann ich dir den Tipp geben, das Minorantenkriterium anzuwenden und an eine sehr bekannte divergente Reihe zu denken.

Korrektur: Falsche Implikation korrigiert.

Lg

Comments

Wie erkennt man, dass $\frac{n}{3^n}$ eine monoton fallende Folge ist?

Ich habe hier das Leibnizkrit.: $\sum\limits_{n=1}^{\infty}{(-1)^n c_n}$

Wie muss ich das jetzt damit ausrechnen bzw. was muss ich anstelle des c_n eingeben?

Wäre es so? $\sum\limits_{n=1}^{\infty}{(-1)^n \frac{3}{3^n}}$? Wenn ja, wie geht es dann weiter?

---

Wir nennen eine Folge $a_n$ monoton fallend, wenn $a_{n} > a_{n+1}$ für alle $n \in \mathbb{N}$ gilt. Hier ist unsere Folge $a_n = \frac{n}{3^n}$. Plotten wir die Folge,

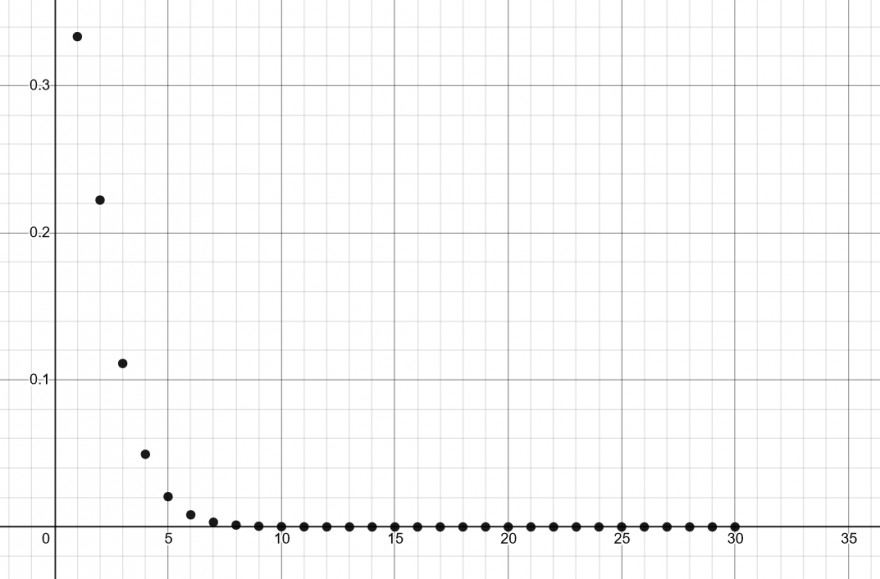
können wir sehen, dass die Folgenglieder einen immer kleineren Wert annehmen. Formal können wir es beweisen, indem wir zeigen, dass

$\frac{n}{3^n} > \frac{n+1}{3^{n+1}}$ bzw., wenn wir das umformen, $3 > \frac{n+1}{n}$ für alle $n \in \mathbb{N}_\geq 1$.

Ich habe hier das Leibnizkrit.: $\sum\limits_{n=1}^{\infty}{(-1)^n c_n}$. Wie muss ich das jetzt damit ausrechnen bzw. was muss ich anstelle des $c_n$ eingeben?

Du rechnest hier gar nichts aus. Das ist ja gerade das besondere an dem Leibniz-Kriterium. In seiner vollen Länge lautet das Kriterium

Sei $(c_n)_{n \in \mathbb{N}}$ eine monoton fallende, reelle Nullfolge, dann konvergiert die alternierende Reihe

$\sum\limits_{n=0}^{\infty} (-1)^nc_n$.

Es genügt also zu zeigen, dass $a_n = \frac{n}{3^n}$ eine monoton fallende Folge ist und gegen $0$ konvergiert. Sind diese beiden Eigenschaften der Folge gegeben, liefert uns dieses Kriterium, dass dann die Reihe konvergieren muss.

Wie du aber sicherlich merkst, ist dein Quotientenkriterium hier ein schnellerer und einfacherer Weg. Es gibt aber auch alternierende Reihen, wo die Folgenglieder dann nicht mehr so einfach mit dem Quotientenkriterium zu berechnen sind - da hilft uns dann das Leibniz-Kriterium. Deshalb wollte ich es dir mal gezeigt haben.

---

es gilt $n < 3^n$ für alle $n \in \mathbb{N}$, womit $\frac{n}{3^n}$ eine monoton fallende Folge ist.

Es ist auch $n<n+1$ aber $\frac n{n+1}$ monoton steigend.

---

Danke Arsinoë4 für den Hinweis. Da war ich kurz unaufmerksam. Hab's korrigiert.