Untersumme gegen unendlich Verständnisfrage

Question

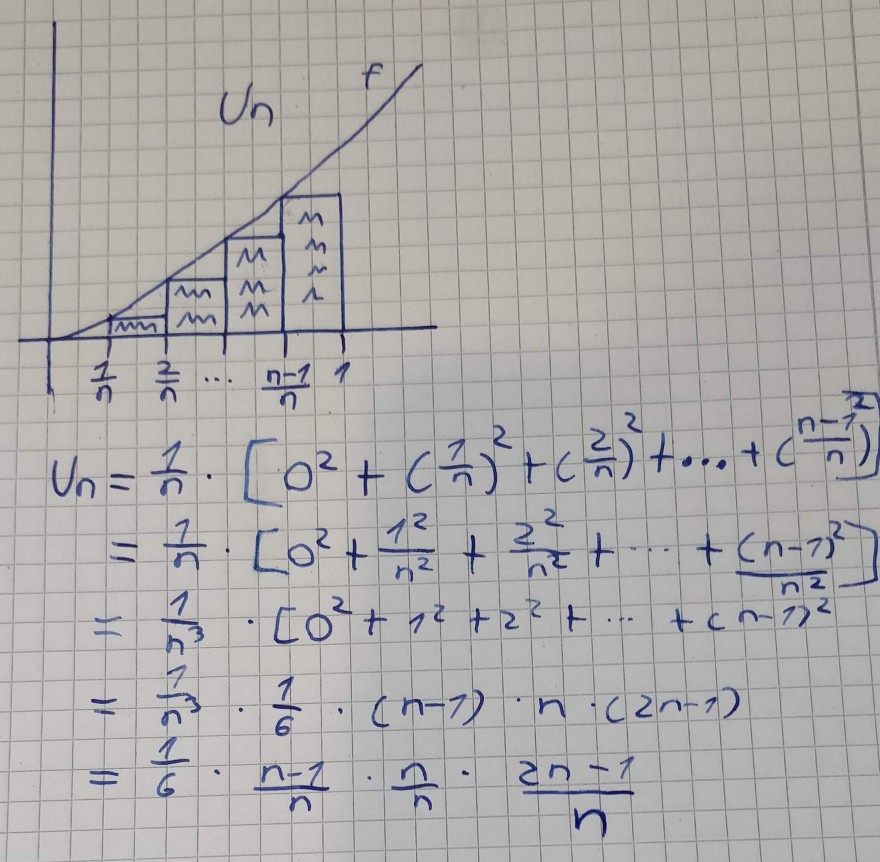
Aufgabe:

Streifenmethode Berechnung für Untersumme gegen unendlich

Problem/Ansatz:

Habe im Mathebuch mir die Berechnung der Untersumme und Obersumme für n gegen unendlich angesehen, kann aber die Rechenschritte ab Zeile 3 überhaupt nicht mehr nachvollziehen. Ich bitte daher um Hilfe.

Was ich Beispielsweise am Anfang direkt nickt verstehe: Ich habe den Ausdruck 1/n^3, welcher mit den ganzen Elementen der eckigen Klammern multipliziert werden muss. Aus welchem Grund sind im nächsten Rechenschritt jeweils das geteilt durch n^2 der Elemente in der Klammer entfernt und dafür steht ganz links nicht mehr 1/n sondern 1/n^3?

Answer 1

Das nennt man "Ausklammern"...

Von der dritten zur vierten Zeile brauchst du die Summenformel für Quadratzahlen. Statt n musst du aber n-1 nehmen.

\( \sum \limits_{i=1}^{n} i^{2}=\frac{n(n+1)(2 n+1)}{6} \)

:-)

Comments

Ich habe meine Antwort ergänzt.

Answer 2

\( \frac{1}{n} \cdot\left[0^{2}+\frac{1^{2}}{n^{2}}+\frac{2^{2}}{n^{2}}+\ldots+\frac{(n-1)^{2}}{n^{2}}\right]= \)

\( =\frac{1}{n} \cdot\left\{\frac{1}{n^{2}} \cdot\left[0^{2}+1^{2}+2^{2}+\ldots+(n-1)^{2}\right]\right\} \)=

\( =\frac{1}{n^{3}} \cdot\left[0^{2}+1^{2}+2^{2}+\ldots+(n-1)^{2}\right] \)

Comments

Alles klar, das habe ich jetzt verstanden. Doch wie kommen im nächsten Schritt die 1/6 ins Spiel?