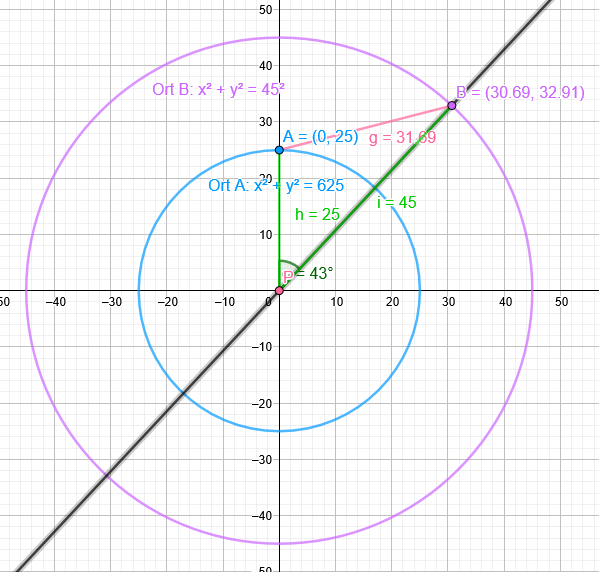
-Berechne die Länge der neuen Straße : (alternativ)
Berechnung der Geraden durch P(0|0) und B:
y=tan(90°-43°)*x≈1,07x
Koordinaten von B:
Kreis um P(0|0) mit r=45 x^2+y^2=45^2
Schnitt mit y=1,07x → B(30,69|32,91)
Ort A hat die Koordinaten A(0|25)
Weiter mit dem Satz des Pythagoras:
\( g=\sqrt{30,69^{2}+(32,91-25)^{2}} \approx 31,693 \mathrm{~km} \)