Bestimmen Sie die Funktion g, auf deren Graph die Hochpunkte von fk liegen

Question

Aufgabe:

Text erkannt:

Aufgabe 1) Gegeben ist die Funktion \( f_{k} \) mit \( f_{k}(x)=x^{2} \cdot e^{k x} \) mit \( k \in \mathbb{R} \).
a) Skizzieren Sie die Graphen von \( f_{k} \) für \( \mathrm{k}=-0,5 ; \mathrm{k}=0 \) und \( \mathrm{k}=1 \) in ein geeignetes Koordinatensystem.
b) Berechnen Sie algebraisch die lokalen Extrema und die Wendepunkte von \( f_{k} \). (Die hinr. Bed. muss nicht überprüft werden)
c) Bestimmen Sie die Funktion g, auf deren Graph die Hochpunkte von \( f_{k} \) liegen.

Problem/Ansatz:

… könnten Sie mir bei Aufgabe c helfen?

Die anderen Aufgabenteile habe ich gemacht.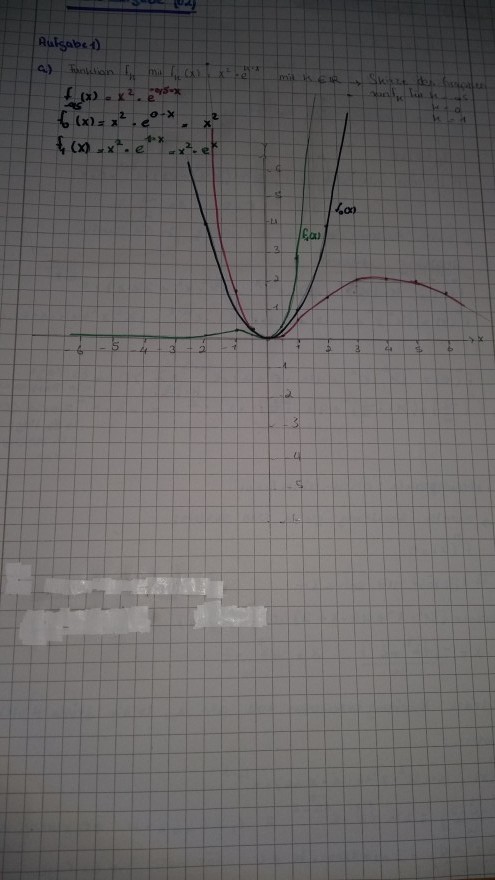

Text erkannt:

1

Answer 1

c)

fk(x) = x^2·e^(k·x)
fk'(x) = e^(k·x)·(k·x^2 + 2·x) = 0
k·x^2 + 2·x = x·(k·x + 2) = 0
x = 0
k·x + 2 = 0 → k = - 2/x

g(x) = x^2·e^((- 2/x)·x) = x^2/e^2

Skizze

~plot~ x^2·e^(-0.5x);x^2·e^(0x);x^2·e^(1x);x^2/e^2;[[-8|8|0|10]] ~plot~