Verständnisfrage zu der Basiswechselmatrix
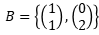
Text erkannt:
\( B=\left\{\left(\begin{array}{l}1 \\ 1\end{array}\right),\left(\begin{array}{l}0 \\ 2\end{array}\right)\right\} \)
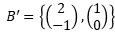
Text erkannt:
\( B^{\prime}=\left\{\left(\begin{array}{c}2 \\ -1\end{array}\right),\left(\begin{array}{l}1 \\ 0\end{array}\right)\right\} \)
gesucht ist: 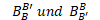
Text erkannt:
\( B_{B}^{B \prime} \) und \( B_{B^{\prime}}^{B} \)
Text erkannt:
\( B_{B}^{B \prime} \) und \( B_{B{\prime}}^{B} \)
Verständnisfragen:
1) Ist der Lösungsweg mit der Identitätsmatrix richtig (wie beim Invertieren)
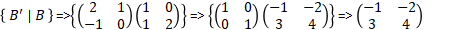
Text erkannt:
\( \left\{B^{\prime} \mid B\right\}=\left\{\left(\begin{array}{cc}2 & 1 \\ -1 & 0\end{array}\right)\left(\begin{array}{ll}1 & 0 \\ 1 & 2\end{array}\right)\right\} \Rightarrow\left\{\left(\begin{array}{cc}1 & 0 \\ 0 & 1\end{array}\right)\left(\begin{array}{cc}-1 & -2 \\ 3 & 4\end{array}\right)\right\} \Rightarrow\left(\begin{array}{cc}-1 & -2 \\ 3 & 4\end{array}\right) \)
2) Wie liest man das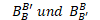 ? wäre die Lösung bei 1)
? wäre die Lösung bei 1) 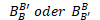 ?
?
Text erkannt:
\( B_{B}^{B \prime} \) und \( B_{B^{\prime}}^{B} \)
3) müssen die Matrizen beim Basiswechsel gleich sein und quadratisch sein?
4) WIe ist das wenn es sich nicht zur Identitätsmatrix umformen lässt?
5) Gibt es noch andere Lösungsmethoden zum Basiswechsel?
vg coffee.cup
Text erkannt:
\( B_{B}^{B \prime} \) und \( B_{B}^{B} \)