Heyy :)
Bräuchte Hilfe bei diesen Aufgaben!
Teilaufgabe a) hab ich schon… ich muss nur noch b), c) und d) machen, verstehe aber nicht wie.
Freue mich auf eure Hilfe
Mfg
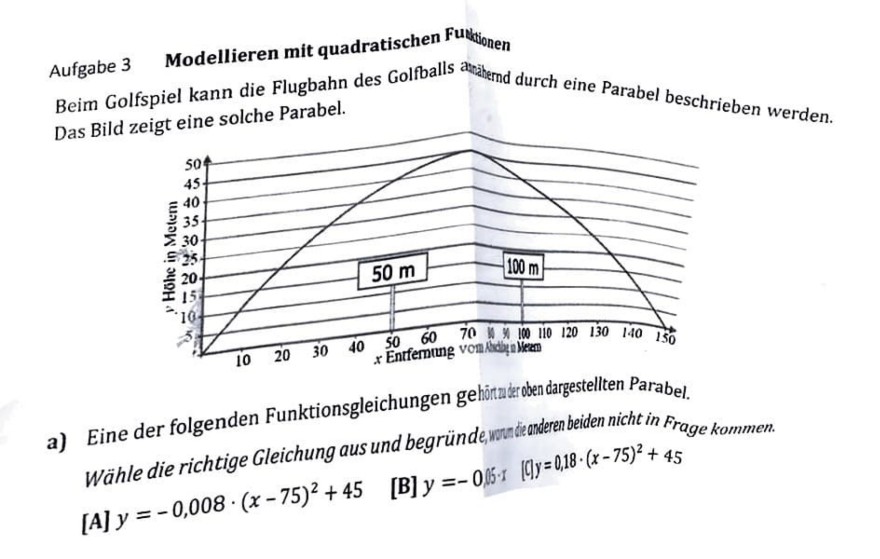
Text erkannt:
Aufgabe 3 Modellieren mit quadratischen Fuধsionen
Beim Golfspiel kann die Flugbahn des Golfballs atpihernd durch eine Parabel beschrieben werden. Das Bild zeigt eine solche Parabel.
a) Eine der folgenden Funktionsgleichungen gehötrisroben dargestellten Parabel.
Wähle die richtige Gleichung aus und begründe,wundienderen beiden nicht in Frage kommen.
[A] \( y=-0,008 \cdot(x-75)^{2}+45 \)
[B] \( y=-0,06-1[] y=0,18 \cdot(x-75)^{2}+45 \)

Text erkannt:
b) Fine andere Flugbahn kann durch die Gleichung
\( y=-0,004 \cdot(x-62,5)^{2}+15,625 \text { beschrieben werden. } \)
1) Berechne, in welcher Höhe sich der Golfball über der \( 50 \mathrm{~m} \)-Markierung befindet.
2) Bestimme rechnerisch, wie weit der Golfball fliegt.
c) Ein Ball, dessen Flugbahn ebenfalls durch eine Parabel beschrieben werden kann, erreicht seine maximale Höhe über der \( 50 \mathrm{~m} \)-Markierung.
Bestimme die Entfernung vom Abschlag bis zum Landepunkt. Begründe deine Antwort.
d) Bei einer vierten Flugbahn erreicht der Ball eine größte Höhe von \( 60 \mathrm{~m} \) und landet bei \( 200 \mathrm{~m} \).
Bestimme eine Funktionsgleichung der Parabel, die diese Flugbahn beschreibt.
Gib die Funktionsgleichung der Parabel in Normalform an.
