Berechnen Sie die Höhe der Pflanze nach 5 Wochen.

Question

Aufgabe:In einer landwirtschaftlichen Versuchsanstalt wird die Höhe einer neu gezüchteten Pflanze zur Produktion von Bio-Diesel in den ersten Wochen ihres Wachstums vermessen. Es wird davon ausgegangen, dass die Pflanze ca. 1 m hoch wird. Rechnen sie mit der Funktionsgleichung N(t)= 100-100e^-0,1054 t weiter. b) Zeichnen Sie den Graphen Funktion in ein Koordinatensystem. c) Berechnen Sie die Höhe der Pflanze nach 5 Wochen. d) Ermitteln Sie, wann die Pflanze die Hälfte der erwarteten Höhe erreicht hat. e) Berechnen Sie das durchschnittliche wöchentliche Pflanzenwachstum von der 2, bis zur 7. Woche. f) Berechnen Sie die durchschnittliche Wachstumsgeschwindigkeit von der 2. bis zur 7. Woche.

Problem/Ansatz: wie löst man alles ?

Answer 1

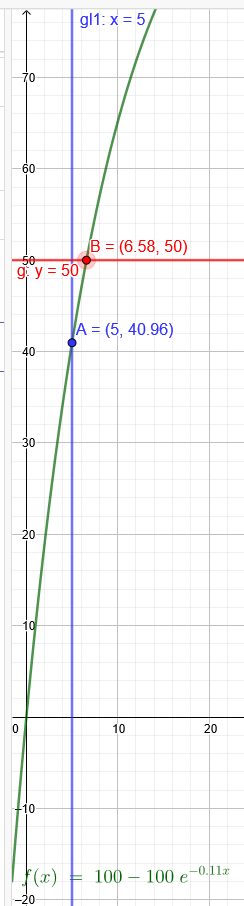
N(t)= 100-100e^-0,1054t

c) Berechnen Sie die Höhe der Pflanze nach 5 Wochen

N(5)= 100-100e^-0,1054*5≈40,96

d) Ermitteln Sie, wann die Pflanze die Hälfte der erwarteten Höhe erreicht hat.

\( 50=100-100 e^{-0,1054 t} \)

\( -50=-100 e^{-0,1054 t} \)

\( 1=2 e^{-0,1054 t} \)

\( \frac{1}{e^{0,1054 t}}=\frac{1}{2} \)

\( e^{0,1054 t}=2 \mid \ln \)

\( 0,1054 \cdot t=\ln 2 \)

\( t=\frac{\ln 2}{0,1054} \approx 6,576 \)