Kannmir da jemand die rechenwege plus Lösung sagen? 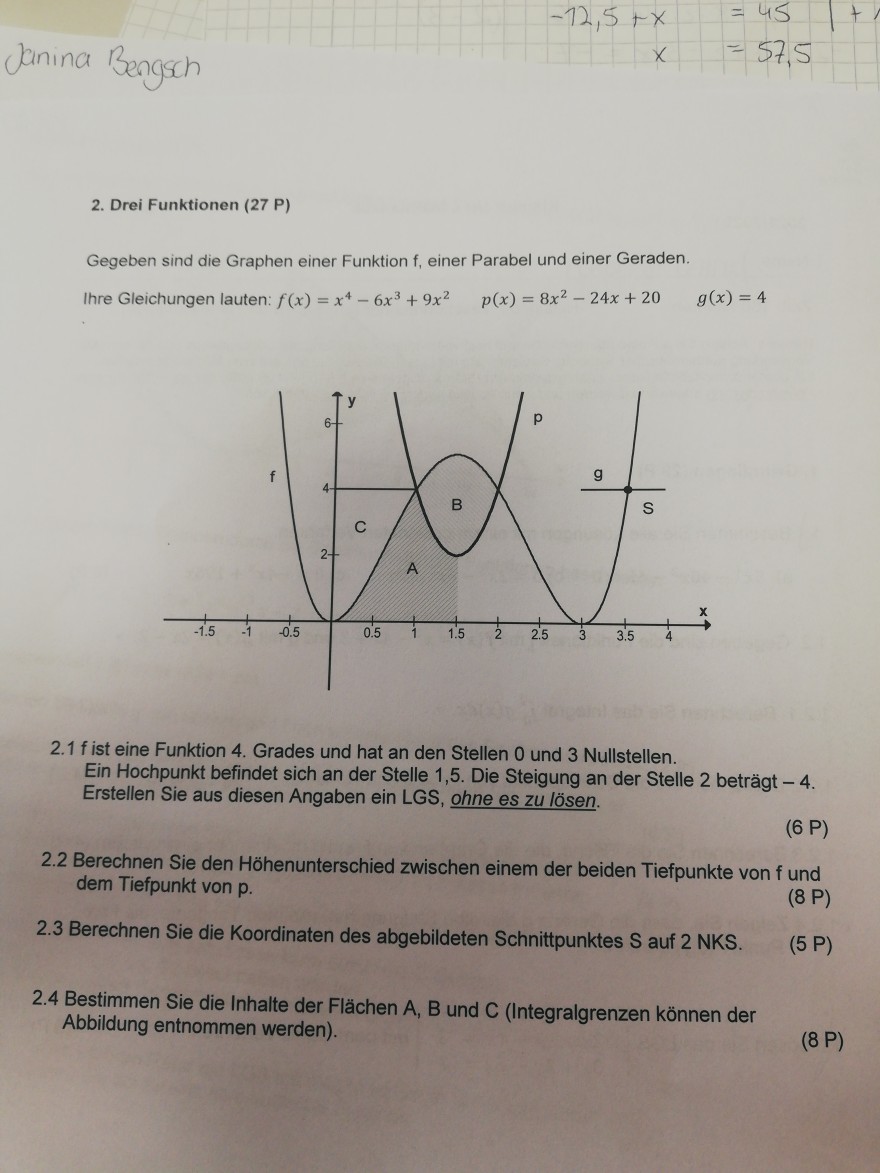
Aufgabe:
2. Drei Funktionen (27 P)
Gegeben sind die Graphen einer Funktion \( \mathrm{f} \), einer Parabel und einer Geraden.
Ihre Gleichungen lauten: \( f(x)=x^{4}-6 x^{3}+9 x^{2} \quad p(x)=8 x^{2}-24 x+20 \quad g(x)=4 \)
\( 2.1 \) f ist eine Funktion 4. Grades und hat an den Stellen 0 und 3 Nullstellen.
Ein Hochpunkt befindet sich an der Stelle \( 1,5 . \) Die Steigung an der Stelle 2 beträgt - \( 4 . \) Erstellen Sie aus diesen Angaben ein LGS, ohne es zu lösen.
(6 P)
\( 2.2 \) Berechnen Sie den Höhenunterschied zwischen einem der beiden Tiefpunkte von \( f \) und dem Tiefpunkt von \( \mathrm{p} \).
(8 P)
2.3 Berechnen Sie die Koordinaten des abgebildeten Schnittpunktes S auf 2 NKS.
(5 P)
\( 2.4 \) Bestimmen Sie die Inhalte der Flächen A, B und C (Integralgrenzen können der Abbildung entnommen werden).
(8 P)