Vom Duplikat:
Titel: Berechnen Sie die erwarteten Kosten des Unternehmens unter der Annahme, dass X eine Zufallsvariable sei mit …
Stichworte: integral,kostenfunktion,erwartungswert
Aufgabe:
Eine Firma habe eine quadratische Kostenfunktion der Form 1000+20X+0.3X2, wobei X die Menge an produzierten Gütern bezeichne. Berechnen Sie die erwarteten Kosten des Unternehmens unter der Annahme, dass X eine Zufallsvariable sei mit Erwartungswert 100 und Standardabweichung 30.
Die Antwortmöglichkeiten:
6750
6480
6120
6270
6030
Problem/Ansatz:
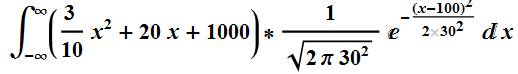
Text erkannt:
\( \int \limits_{-\infty}^{\infty}\left(\frac{3}{10} x^{2}+20 x+1000\right) * \frac{1}{\sqrt{2 \pi 30^{2}}} e^{-\frac{(x-100)^{2}}{2 \times 30^{2}}} d x \)
Ich weiß, dass diese Formel mit integral dafür existiert, bei der Prüfung ist allerdings nur ein Taschenrechner ohne Integral-Rechenfunktion erlaubt. Wie kann man das daher ohne diese Funktion ausrechnen?
Vielen lieben Dank im Voraus!