Maximale Höhe berechnen

Question

Aufgabe:

Text erkannt:

15. Bel einer Wurfparabel wird die maximale Wurfweite immer bei einem Abwurfwinkel von $45^{\circ}$ erreicht. Zudem hängt diese maximale Wurfweite natürlich von der Anfangsgeschwindigkeit der Kugel, also von der Kraft des Sportlers ab. Ein Kugelstoßer stößt aus einer Höhe von 2 m und unter einem Winkel von $45^{\circ}$ die Kugel $12 \mathrm{~m}$ (15 m, $18 \mathrm{~m}$ ) weit. Berechnen Sie jeweils die maximale Höhe der Flugbahn.

Problem/Ansatz:

Kann jemand mir bei dieser Aufgabe helfen:(

Answer 1

Hallo

" Bel einer Wurfparabel wird die maximale Wurfweite immer bei einem Abwurfwinkel von $45^{\circ}$ erreicht." gilt nur bei Abwurf aus Höhe 0 nicht aus Höhe 2m.

allgemeine Parabel hinschreiben, 2 Punkte (0,2) und (12,0) bekannt außerdem f'(0)=1

damit die Parabel bestimmen und dann den Scheitel . (danke für die Verbesserung von Gast)

Gruß lul

Comments

Deshalb weiss ich nicht, ob die "Wurfweite bis wieder 2m oder die echte ist.
Dann sieh dir die Skizze an.

Im übrigen ist dies tatsächlich eine Mathe-Frage.

---

Danke, ich habe editiert.

lul

Answer 2

f(x)=ax²+bx+c

f'(x)=2ax+b

f(0)=2 → c=2

f'(0)=1 → b=1

Also

f(x)=ax²+x+2

f(w)=0 → aw²+w+2=0 → a=(-w-2)/w²

--> f(x)=(-w-2)/w² *x²+x+2

f'(x)=2*(-w-2)/w² *x +1

2*(-w-2)/w² *x_H +1=0

xH=w²/(2w+4)

w=12 → xH=144/28=36/7

          yH=-7/72 * (36/7)²+36/7+2

               =50/7-18/7=32/7=4,57...

Wolframalpha zur Kontrolle:

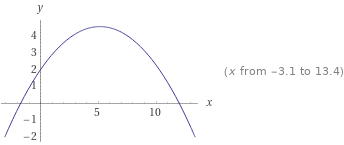
$\max \left\{\frac{(-w-2) x^{2}}{w^{2}}+x+2 \mid w=12\right\}=\frac{32}{7}$ at $(w, x)=\left(12, \frac{36}{7}\right)$

 $\max \left\{\frac{(-w-2) x^{2}}{w^{2}}+x+2 \mid w=15\right\} \approx 5.30882$ at $(w, x) \approx(15,6.61765)$

$\max \left\{\frac{(-w-2) x^{2}}{w^{2}}+x+2 \mid w=18\right\}=6.05$ at $(w, x)=(18,8.1)$

:-)