Hallo Charly,
ich war mir erst nicht sicher, aber die Konstruktion ist identisch zu der beim geraden Kegel. Man muss lediglich beachten, dass der 'korrespondierende' Schnittkreis parallel zum Grundkreis liegt und nicht senkrecht auf der Kegelachse steht.
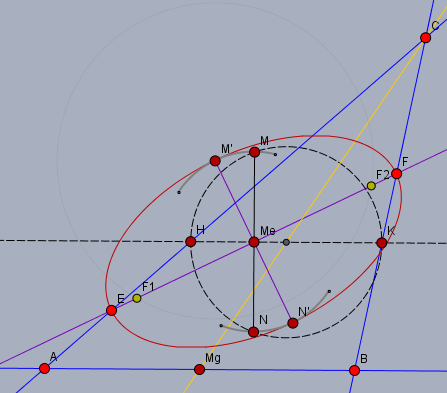
Der Unterschied zur Skizze in der letzten Aufgabe besteht noch darin, dass ich die Ellipse in ihre Schnittebene gekippt habe. Vielleicht kannst Du es Dir dann besser vorstellen, wie's gemeint ist. Das ändert aber rein gar nichts an der Aussage und hat auch nichts mit schiefer oder gerader Kegel zu tun.
In diesem Fall geht eine Halbachse von \(M_e\) (dem Mittelpunkt der Ellipse) bis \(F\) und die andere von \(M_e\) nach \(M'\).
Die Halbachse \(M_eM'\) muss aber gar nicht die Kürzere sein. Siehe folgende Skizze:
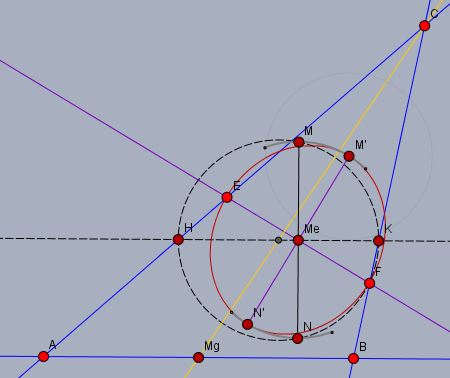
Man muss nur den Schnittwinkel 'umlegen'. So ist \(|M_eM| \gt |M_eF|\).
Bleibt noch zu erwähnen, dass die gelbliche Gerade nicht die Kegelachse ist. Sie geht durch die Mittelpunkte aller waagerechten Schnittkreise.Die Kegelachse wäre die Winkelhalbierende zweier gegenüber liegender Mantellinien (nicht eingezeichnet).
Falls Du Fragen hast, einfach melden.
Gruß Werner
PS.: wozu brauchst Du das eigentlich?