Aufgabe:
…
Problem/Ansatz:
Ich habe a gelöst, aber habe ich b) leider nicht gelöst, so bitte kann jemand die Lösungen von 2b) schicken!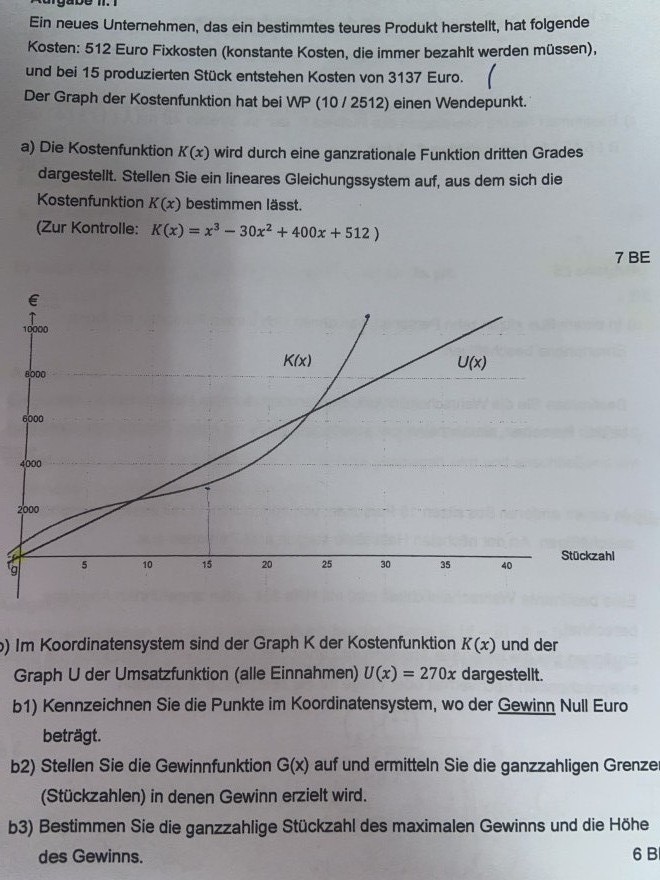
Text erkannt:
Ein neues Unternehmen, das ein bestimmtes teures Produkt herstellt, hat folgende Kosten: 512 Euro Fixkosten (konstante Kosten, die immer bezahlt werden müssen), und bei 15 produzierten Stuck entstehen Kosten von 3137 Euro.
Der Graph der Kostenfunktion hat bei WP (10/ 2512) einen Wendepunkt.
a) Die Kostenfunktion \( K(x) \) wird durch eine ganzrationale Funktion dritten Grades dargestellt. Stellen Sie ein lineares Gleichungssystem auf, aus dem sich die Kostenfunktion \( K(x) \) bestimmen lässt.
(Zur Kontrolle: \( \left.K(x)=x^{3}-30 x^{2}+400 x+512\right) \)
Stückzahl
Im Koordinatensystem sind der Graph \( K \) der Kostenfunktion \( K(x) \) und der Graph U der Umsatzfunktion (alle Einnahmen) \( U(x)=270 x \) dargestellt.
b1) Kennzeichnen Sie die Punkte im Koordinatensystem, wo der Gewinn Null Euro beträgt.
b2) Stellen Sie die Gewinnfunktion \( \mathrm{G}(\mathrm{x}) \) auf und ermitteln Sie die ganzzahligen Grenze (Stückzahlen) in denen Gewinn erzielt wird.
b3) Bestimmen Sie die ganzzahlige Stückzahl des maximalen Gewinns und die Höhe des Gewinns.