1.2 bestimmen sie den Zeitpunkt , an dem die Konzentration ihren maximalen Wert erreicht:
f(x)=12x*\( e^{-0,5x} \)
f´(x)=12*\( e^{-0,5x} \)+12x*(-0,5)*\( e^{-0,5x} \)=12*\( e^{-0,5x} \)-6x*\( e^{-0,5x} \)
12*\( e^{-0,5x} \)-6x*\( e^{-0,5x} \)=0
\( e^{-0,5x} \)*(12-6x)=0 \( e^{-0,5x} \) kann nicht 0 werden.
(12-6x)=0
x=2
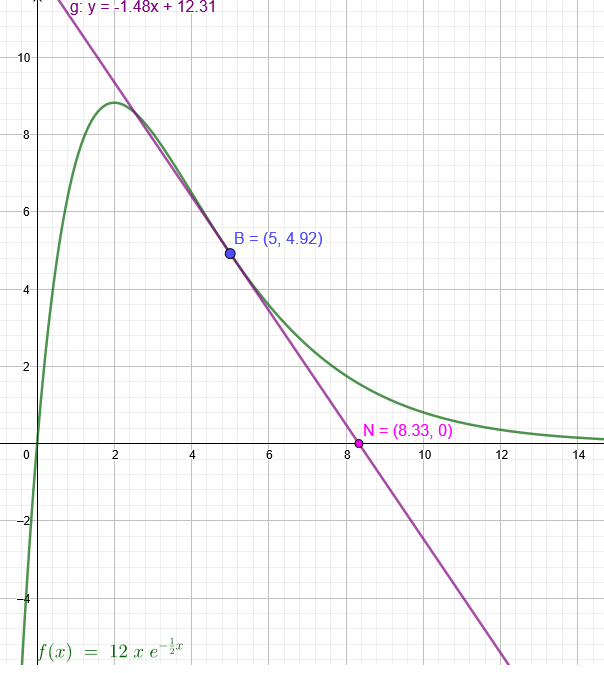
1.3 der lineare Abbau nach 5 Stunden wird durch die Funktion g beschreiben , die durch die Gleichung der Tangente an den Graphen der Funktion f beschrieben wird. Bestimmen sie den Funktionsterm der Funktion.
f´(5)=12*\( e^{-0,5*5} \)-6*5*\( e^{-0,5*5} \)=12*\( e^{-2,5} \)-30*\( e^{-2,5} \)=-18*\( e^{-2,5} \)≈-1,477
f(5)=12*5*\( e^{-0,5*5} \)=60*\( e^{-2,5} \)≈4,92
Berührpunkt der Tangente: B(5|4,92)
Tangentengleichung:
\( \frac{y-4,92}{x-5} \)=-1,477
y-4,92=-1,477x+7,385
y=-1,477x+12,305
1.4 Bestimmen Sie den Zeitpunkt, zu dem die Konzentration auf Null gesunken ist.
y=-1,477x+12,305
-1,477x+12,305=0
x=8,33...