Einsteinische Summenkonvektion - Kronecker Delta

Question

Aufgabe:

Mit der Anwendung von einsteinischen Summenkonvektion vereinfachen

Problem/Ansatz:

Man soll folgende Aufgabe mit dieser Bedingung Vereinfachen: (u,u)=1

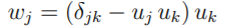
Man soll folgendes berechnen/ vereinfachen - mit der einsteinschen Summenkonvektion.

Was ich nicht verstehe: Was wurde mit der obigen Bedingung (u,u)=1 gemeint?

Ich weiss, dass Kronecker delta gleich 1 ist, wenn j=k und gleich 0, wenn j und k unglech sind.

Wie kann ich aber mit diesem die Gleichung lösen?

Danke für eure Tipps!

Answer 1

Aloha :)

Über doppelt auftretende Indizes wird summiert. Hier ist der eine Faktor die Klammer und der zweite Faktor das \(u_k\) hinter der Klammer. Der doppelt auftretende Index ist daher \(k\):

$$w_j=\left(\delta_{jk}-u_ju_k\right)u_k=\sum\limits_{k=1}^n\left(\delta_{jk}-u_ju_k\right)u_k=\sum\limits_{k=1}^n\delta_{jk}u_k-u_j\sum\limits_{k=1}^nu_ku_k$$Wegen \(\left<\vec u\,|\,\vec u\right>=1\) ist die letzte Summe gleich \(1\). Die erste Summe fällt weg, weil \(\delta_{jk}\) für fast alle \(k\) aus der Summe \(0\) ist, nur nicht für \(k=j\), da hat es den Wert \(1\). Die erste Summe können wir daher durch \(u_j\) ersetzen.$$w_j=u_j-u_j\cdot1=0$$

Comments

Hallo Tschakabumba,

danke für deine Antwort.

Kannst du bitte noch erklären, wieso wir die erste Summe durch u_j ersetzen können?

Wenn j=k wäre, dann müsste sich dch ergeben u_k-u_j, oder?

Wenn j ungleich k wäre, dann -u_j

Nochmal danke für deine Antwort!

---

Ja, kein Problem. Das Kronecker-Delta ist so definiert:$$\delta_{jk}=\left\{\begin{array}{c}1&\text{falls }j=k\\0&\text{falls }j\ne k\end{array}\right.$$

Damit lautet die Summe:$$\sum\limits_{k=1}^n\delta_{jk}\cdot u_k=\delta_{j1}\cdot u_1+\delta_{j2}\cdot u_2+\delta_{j3}\cdot u_3+\cdots+\delta_{jn}\cdot u_n$$In der Summe sind alle Kronecker-Deltas \(=0\), bis aus das eine, bei dem die Indizes gleich sind. Daher bleibt genau \(u_j\) übrig.

---

alles klar, danke!