Komme mit folgender Aufgabe nicht weiter:
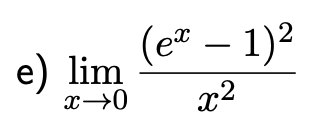
Text erkannt:
e) \( \lim \limits_{x \rightarrow 0} \frac{\left(e^{x}-1\right)^{2}}{x^{2}} \)
Berechnet werden soll der Grenzwert mit l'Hospital. Das hab ich in meinem Rechenweg gekennzeichnet, alles andere sind nur Vereinfachungen.
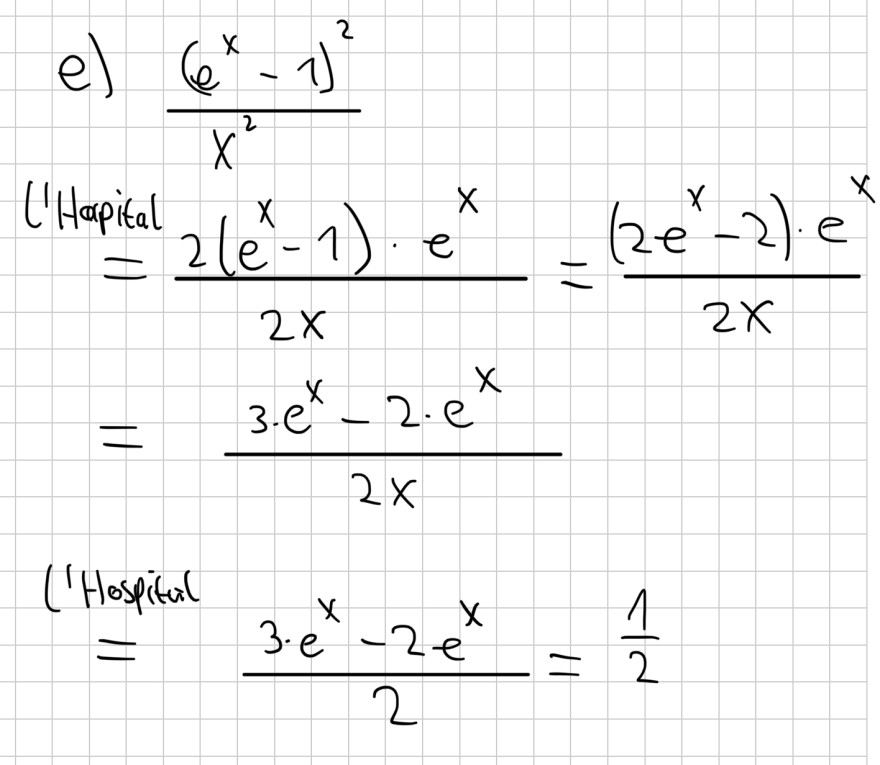
Text erkannt:
e) \( \frac{\left(e^{x}-1\right)^{2}}{x^{2}} \)
('Hapital \( \frac{2\left(e^{x}-1\right) \cdot e^{x}}{2 x}=\frac{\left(2 e^{x}-2\right) \cdot e^{x}}{2 x} \)
\( =\frac{3 \cdot e^{x}-2 \cdot e^{x}}{2 x} \)
('Hositul \( \frac{3 \cdot e^{x}-2 e^{x}}{2}=\frac{1}{2} \)
Komme auf 1/2, die Lösung sagt aber 1. Wie kann das sein?
x^2 ist doch immer abgeleitet 2x und dann 2, was ja die Bedingung für l'Hospital nicht mehr erfüllen würde, also muss man da doch stoppen. Sehe da keinen anderen Weg...