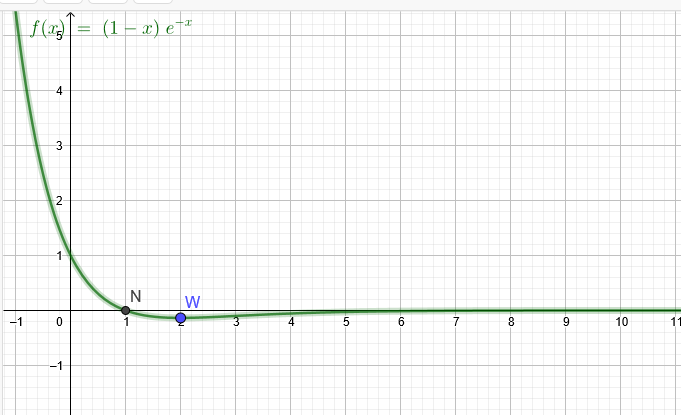
\( f(x)=(1-x) \cdot e^{-x}=\frac{1-x}{e^{x}} \) wobei der Nenner nicht 0 werden \( \operatorname{kann}(\rightarrow \) keine Polstelle)
Nullstelle: \( f(x)=0 \)
\( \begin{array}{l} \frac{1-x}{e^{x}}=0 \\ 1-x=0 \end{array} \)
\( x=1 \)
Schnitt mit der \( y \)-Achse \( f(0)=\frac{1-0}{e^{0}}=1 \)
Extremwerte: \( f \cdot(x)=0 \)
\( \begin{array}{l} f \cdot(x)=\frac{-1 \cdot e^{x}-(1-x) \cdot e^{x}}{\left(e^{x}\right)^{2}}=\frac{-1-(1-x)}{e^{x}}=(-1-1+x) \frac{)}{e^{x}}=\frac{x-2}{e^{x}} \\ x-2=0 \\ x=2 \rightarrow f(2)=\frac{1-2}{e^{2}}=-\frac{1}{e^{2}} \approx-0,1353 \end{array} \)
Art des Extremwertes:
\( \begin{array}{l} f^{\prime \prime}(x)=\frac{1 \cdot e^{x}-(x-2) \cdot e^{x}}{\left(e^{x}\right)^{2}}=\frac{1-(x-2)}{e^{x}}=(1-x+2) \frac{)}{e^{x}}=\frac{3-x}{e^{x}} \\ f^{\prime \prime}(2)=\frac{3-2}{e^{2}}=\frac{1}{e^{2}}>0 \rightarrow \text { Minimum } \end{array} \)
Wendepunkt: \( f \cdot(x)=0 \)
\( x=3 \rightarrow f(3)=\frac{1-3}{e^{3}}=-\frac{2}{e^{3}} \approx-0,099 \)
\( 3-x=0 \)