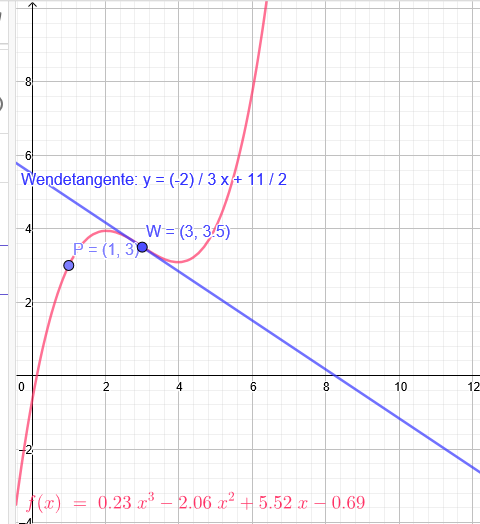
10b) Der Graph verläuft durch den Punkt P(1|3) und x=3 ist eine Wendestelle von f. Die zugehörige Wendetangente hat die Gleichung y=-2/3x + 11/2
f(x)=a*x^3+b*x^2+c*x+d
P(1|3)
f(1)=a*1^3+b*1^2+c*1+d
1.)a+b+c+d=3
Wendetangente:
y=-2/3x + 11/2 → x=3 ist eine Wendestelle → y=-2/3*3 + 11/2=-2+5,5=3,5
Wendepunkt W(3|3,5)
f(3)=a*3^3+b*3^2+c*3+d
2.)27a+9b+3c+d=3,5
Tangentensteigung m=-2/3 bei W(3|3,5)
f´(x)=3ax^2+2bx+c
f´(3)=3a*3^2+2b*3+c
3.) 27a+6b+c=-2/3
Wendepunkteigenschaft:
f´´(x)=6ax+2b
f´´(3)=6a*3+2b
4.)18a+2b=0
a≈0,229 b≈-2,06 c≈5,52 d ≈-0,687
f(x)=0,229x^3-2,06x^2+5,52x-0,687