Steckbriefaufgabe : Bestimmen Sie eine ganzrationale Funktion 3. Grades

Question

Aufgabe: Bestimmen Sie eine ganzrationale Funktion 3. Grades, die im Punkt A(1| 4) eine Stelle mit waagerechter Tangente und in B(0 | 2) einen Wendepunkt hat.
Weisen Sie anschließend rechnerisch nach, ob es sich bei A um einen Hoch- oder Tiefpunkt handelt.

Problem/Ansatz:

Ich bin komplett lost um ehrlich zu sein . Grundsätzlich habe ich ja 2 Infos gegeben: - f(1)=4 & f(0)=2 . Aber wie mache ich dann weiter??? Ich denke hier soll mit linearen Gleichungssystemen gearbeitet werden

Answer 1

eine Stelle mit waagerechter Tangente

Das heißt die Steigung ist dort 0. Also f'(1) = 0.

einen Wendepunkt

Das heißt die zweite Ableitung ist dort 0. Also f''(0) = 0.

Answer 2

Grundsätzlich habe ich ja 2 Infos gegeben:

Du hast 4 Informationen gegeben!

im Punkt A(1| 4) eine Stelle mit waagerechter Tangente

heißt auch: f '(1)=0.

in B(0 | 2) einen Wendepunkt

heißt auch: f ''(0)=0.

Answer 3

Hallo,

f(x)=ax³+bx²+cx+d

f(0)=2 = d

f(1)=4=a+b+c+2 → a+b+c=2

Nun brauchst du noch die beiden Ableitungen und benutzt die Bedingungen aus den anderen Antworten.

f'(x)= ...

f'(1)=0= ...

f''(x)= 6ax+b

f''(0)=0=b

Es bleiben zwei Gleichungen, mit denen du a und c berechnest.

:-)

Answer 4

Aloha :)

Willkommen in der Mathelounge... \o/

Die Gesuchte ist eine ganzrationale Funktion 3-ten Grades:$$\pink{f(x)=ax^3+bx^2+cx+d}$$$$f'(x)=3ax^2+2bx+c$$$$f''(x)=6ax+2b$$

Im Punkt \(B(0|2)\) hat sie einen Wendepunkt. Daraus folgt$$(c)\quad2=f(0)=d\implies\pink{d=2}$$$$(d)\quad0=f''(0)=2b\implies\pink{b=0}$$

Im Punkt \(A(1|4)\) hat sie eine waagerechte Tangente. Daraus folgt$$(a)\quad 4=f(1)=a+\pink b+c+\pink d=a+c+2\implies \green{a+c=2}$$$$(b)\quad0=f'(1)=3a+2\pink b+c=3a+c=2a+(\green{a+c})=2a+\green2\implies\pink{a=-1}$$

Aus \(\green{a+c=2}\) und \(\pink{a=-1}\) folgt \(\pink{c=3}\) und wir haben die Gesuchte gefunden:$$\pink{f(x)=-x^3+3x+2}$$

Da bei \(A(1|4)\) eine waagerechte Tangente vorliegt, ist dieser Punkt ein Kandidat für ein Extremum. Wir prüfen den Kandidaten, indem wir die zweite Ableitung an diesem Punkt bestimmen:$$f''(1)=\left(-x^3+3x+2\right)''_{x=1}=\left(-3x^2+3\right)'_{x=1}=\left(-6x\right)_{x=1}=-6<0\implies\text{Maximum}$$Am Punkt \(A(1|4)\) liegt also ein lokales Maximum vor.

~plot~ -x^3+3x+2 ; {1|4} ; {0|2} ; [[-4|4|-6|6]] ~plot~

Answer 5

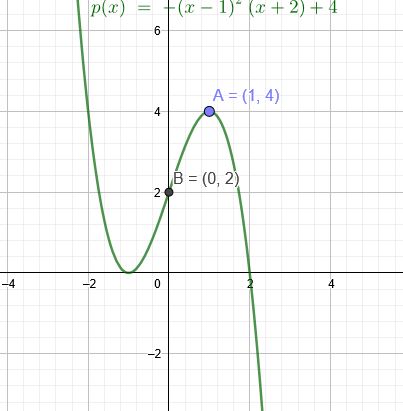
"Bestimmen Sie eine ganzrationale Funktion 3. Grades, die im Punkt \(A(1| 4)\) eine Stelle mit waagerechter Tangente und in \(B(0 | 2)\) einen Wendepunkt hat.
Weisen Sie anschließend rechnerisch nach, ob es sich bei A um einen Hoch- oder Tiefpunkt handelt."

Ich verschiebe den Graphen von \(f(x)\) um 4 Einheiten nach unten:

\(A(1| 4)\)→\(A´(1| 0)\) waagerechte Tangente  

\(B(0 | 2)\)→\(B´(0 | -2)\) Wendepunkt

\(f(x)=a*[(x-1)^2*(x-N)]\)

\(f(0)=a*(0-1)^2*(0-N)=-2\)     →  \(a=\frac{2}{N}\)

\(f(x)=\frac{2}{N}*[(x-1)^2*(x-N)]\)

\(f´(x)=\frac{2}{N}*[(2x-2)*(x-N)+(x-1)^2]\)

\(f´´(x)=\frac{2}{N}*[(2)*(x-N)+(2x-2)+(2x-2)]\)  →  \(f´´(x)=\frac{4}{N}*[(2x-2N)+(4x-4)]\)

\(f´´(0)=\frac{2}{N}*[(-2N)+(0-4)]=0\)    →\(N=-2\)   →  \(a=-1\)

\(f(x)=-1*[(x-1)^2*(x+2)]\) und nun wieder 4 Einheiten nach oben:

\(p(x)=-1*[(x-1)^2*(x+2)]+4\)

2 Nachweise: \(A(1| 4)\) ob Hoch oder Tiefpunkt:

1.)\(p(x)=-1*[(x-1)^2*(x+2)]+4\)

\(p´(x)=-1*[(2x-2)*(x+2)+(x-1)^2]\)

\(p´´(x)=-1*[2*(x+2)+(2x-2)+(2x-2)]\)

\(p´´(1)=-1*[2*(1+2)+(2*1-2)+(2*1-2)]\)

\(p´´(1)=-1*[6+0-1]\)      \(-5<0\)  Maximum

2.)Extremwert bei:\(A(1| 4)\)   und Wendestelle bei: \(B(0 | 2)\)

Der Wendepunkt liegt 2 Einheiten tiefer als der Extremwert. Somit ist \(A(1| 4)\) ein lokales Maximum.

Answer 6

Bestimmen Sie eine ganzrationale Funktion 3. Grades,

f(x) = ax³ + bx² + cx + d

die im Punkt A(1| 4) eine Stelle mit waagerechter Tangente

f(1) = 4
f'(1) = 0

und in B(0 | 2) einen Wendepunkt hat.

f(0) = 2
f''(0) = 0

Weisen Sie anschließend rechnerisch nach, ob es sich bei A um einen Hoch- oder Tiefpunkt handelt.

Nutze zur Hilfe und Selbstkontrolle die Seite http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

Gleichungssystem

a + b + c + d = 4
3a + 2b + c = 0
d = 2
2b = 0

Errechnete Funktion

f(x) = -x^3 + 3·x + 2

Man erkennt, dass der Punkt A ein Hochpunkt ist.