Die Lage von zwei Ebenen, wie geht man vor?

Question

Aufgabe:

Die Ebenen E und F schneiden sich. Bestimmen Sie eine Gleichung der Schnittgeraden g. Stellen Sie eine der Ebenen erforderlichenfalls in Parameterform dar. Zeichnen Sie ein Schragbild.

a)  E: x (vektor) =( 2, 0,0) +r (-1,0,3) +s (-1,4,0)

F: 2x+y+2z =8

b)  E durch A (0/0/0), B (1/2/2), C(-1/0/6)

F: x+y+z=5

c) E: x+2y+z= 4

F: x+y+z =2

Problem/Ansatz:

Answer 1

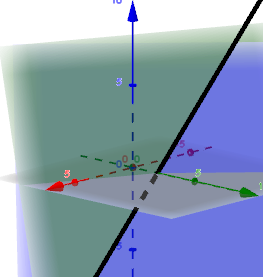
Die Schnittgerade

a) Setze die Parameterform E in F ein

Edit: 2x+y+2z-8 = 0

\( 2( -r - s + 2)+  4 \; s + 2(3 \; r)  -8 = 0  \) 

==> s=

s Einsetzen in E, r wird Parameter der Geraden

==>

\( X: g(r) \, =    \, \left(r, -8 \; r + 8, 3 \; r \right)\)

c)

lege z.B. z=t als Parameter der Geraden fest.

und löse das LGS

\(  t + x + 2 \; y = 4, \\ t + x + y = 2  \)

I-II:==> y=2 ==> x=-t

\(X: g(t) \, =  \, \left(-t, 2, t \right)\)

b) analog nach einem der beiden Fälle

Mußt Du auf Papier zeichnen ?

Würde ich die Spurpunkte bestimmen....

Oder kannst Du mit einer App arbeiten: GeoGebra?

Answer 2

Hallo

was kannst du nicht? die Ebene in Parameterform? Die 2  Ebenen schneiden?

durch 3 Punkte eine Ebene legen?

du musst schon genauer fragen, wir wollen ja nicht einfach 3 HA für dich lösen.

Die Zeichnung kannst du auch mit Geoknecht 3d machen, oder geogebra 3d

Gruß  lul

Comments

Die Zeichnung kannst du auch mit Geoknecht 3d machen

so einfach ist das nicht ;-)  klick hier für a)

---

Ich weiß nicht, wie ich vorgehen soll.

---

Wobei genau hast du Schwierigkeiten, bei der Berechnung?

---

Hab x= 2-1+s

Y= 4s

Z= 3r

--> 2(-2-r-s)+ 1 (4s)+ 2(3r)

2-4-2r-2s+4s+6r

-4+2s+4r =0      /+4

2s+4r      = 4

S= 2-2r

G:x (vektor)= (2,0,0)+r(-1,0,3)+(2-2r) =(-1,4,0)

Und mehr habe ich nicht geschafft.

---

Du setzt dein Ergebnis in E ein

\( \begin{aligned} & 3=2-2 r \\ s: \;& \vec{x}=\left(\begin{array}{l}2 \\ 0 \\ 0\end{array}\right)+r\left(\begin{array}{c}-1 \\ 0 \\ 3\end{array}\right)+(2-2 r)\left(\begin{array}{c}-1 \\ 4 \\ 0\end{array}\right) \\=&\left(\begin{array}{l}2 \\ 0 \\ 0\end{array}\right)+r\left(\begin{array}{c}-1 \\ 0 \\ 3\end{array}\right)+r\left(\begin{array}{c}2 \\ -8 \\ 0\end{array}\right)+\left(\begin{array}{c}-2 \\ 8 \\ 0\end{array}\right) \\=&\left(\begin{array}{l}0 \\ 8 \\ 0\end{array}\right)+r\left(\begin{array}{c}1 \\ -8 \\ 3\end{array}\right) \end{aligned} \)

und erhältst damit die Gleichung der Schnittgeraden s.

---

hallo

was du hast ist doch ganz schön, nur jetzt musst d aes was bei r steht zusammenfassen  und die absoluten Vektoren auch, denn eigentlich steht da schon die Gerade nur sehr unübersichtlich.

zB.  r(-1,0,3)-2r*(-1,4,0)=r*(1,-8,3)

(2,0,0)+2*(-1,4,0)=(0,8,0)

Gruß lul