Aloha :)
Willkommen in der Mathelounge... \o/
Da die Konvergenz der Folge \((a_n)\) vorausgesetzt wird, können wir ihren Grenzwert \(a\) direkt bestimmen, indem wir auf beiden Seiten der Definitionsgleichung den Grenzwert bilden:$$a_{n+1}=\frac34a_n+6\quad\implies\quad\lim\limits_{n\to\infty}a_{n+1}=\lim\limits_{n\to\infty}\left(\frac34a_n+6\right)$$
Da wir die Konvergenz von \((a_n)\) vorausgesetzt haben, können wir den Grenzwert auf der rechten Seite zerlegen:$$\left.\lim\limits_{n\to\infty}a_{n+1}=\frac34\left(\lim\limits_{n\to\infty}a_n\right)+6\quad\right.$$
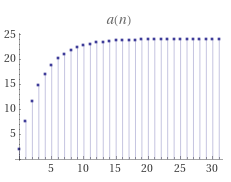
Der Grenzwert von \((a_{n+1})\) und \((a_n)\) ist derselbe:$$a=\frac34a+6\quad\implies\quad\frac14a=6\quad\implies\quad a=24$$