Victor P. Habermann hat 2007 ein kleines Buch veröffentlicht mit dem Titel: „Warum Taschenrechner im Mathematikunterricht nichts zu suchen haben und andere Nestbeschmutzungen“. Darin schreibt er auf Seite 83: „Es ist nicht nur ein hochtrabender Unfug, dem Schüler der ersten Klasse in seinem Zeugnis Erfolge im Fach Mathematik zu bescheinigen, es führt auch zu lang anhaltender Verwechselung“.
Tatsächlich sind die ersten Schritte in die Mathematik wohl überwiegend dem Rechnenlernen gewidmet, was leider in der Unterrichtpraxis dazu führt, dass den Schüler*innen große Aufgabensammlungen angeboten werden mit dem Ziel, das Rechnen so weit zu automatisieren, dass Aufgaben wie 25 – 12 oder 7·8 in einer Sekunde gelöst werden können. Ein Unterricht mit diesem Ziel ist selbstverständlich kein Mathematikunterricht und ein/e Schüler*in der/die nur diese reine Trainingsform des Rechnens kennengelernt hat, erfährt nicht, was Mathematik ihrem Wesen nach ist.
Wie aber muss ein Unterricht aussehen, der zwar dem Rechnenlernen dient und trotzdem die Bezeichnung „Mathematikunterricht“ verdient? Während in einem reinen Rechenunterricht das kleine Einmaleins abgefragt wird, wie im Sprachunterricht Vokabeln, könnte der/die Unterrichtende Handlungen anregen, welche auf das Wesen der Mathematik verweisen. Dazu gehört insbesondere das Zurückführen von neuem Wissen auf bereits erworbenes Wissen. An die Stelle des Auswendig-Lernens des kleinen Einmaleins tritt dann das auswendige Wissen lediglich der Quadratzahlen, das Verdoppeln und das Halbieren sowie die Rückführung von Multiplikationen auf Additionen (bzw. Subtraktionen). Darüber hinaus ist die Mustererkennung eine zentrale, wesenstypische Handlung des Mathematiktreibens. Im Zusammenhang mit der Multiplikation können Kinder entdecken, dass Faktoren vertauscht werden können, wobei das Produkt erhalten bleibt.
Exemplarisch führen wir am Beispiel des 1×7 vor, wie mit den Handlungen Halbieren und Verdoppeln alle Produkte des 1×7 aus den Quadratzahlen und einfachen Additionen (Subtraktionen) gewonnen werden können:
1·7=7
2·7 verdoppeln
3·7 verdoppeln + 7
4·7 verdoppeln und nochmal verdoppeln
5·7 halbieren von 10·7
6·7 halbieren von 10·7 plus 7
7·7 auswendig
8·7 = 7·7+7
9·7 =10·7 – 7
10·7 anhängen einer 0 an die 7.
Natürlich ist ein Kind, das so rechnet einem Kind, welches das 1×7 wie Vokabeln auswendig gelernt hat, im Wettrechnen hoffnungslos unterlegen. Aber es hat schon früh einen Einblick in das Wesen der Mathematik bekommen.
Die lang anhaltende Verwechslung des Rechnens mit der Mathematik hat bei einigen Didaktikern und in vielen Erlassen von Bildungsbehörden dazu geführt, das oft nicht unterscheiden wird, zwischen dem Rechnen im Rahmen einer Aufgabenlösung und der Bedeutung des Rechnens für den Einblick in das Wesen der Mathematik. An dieser mangelhaften Unterscheidung leidet oft auch die Entscheidung, das Rechnen dem elektronischen Werkzeug zu überlassen, ohne beispielsweise zuvor über Rechenvereinfachungen nachzudenken. Ein Beispiel:
Im Rahmen der Einführung der Integralrechnung soll die Fläche unter dem Graphen von f(x)=x2 über dem Intervall [0; a] durch Zerlegung in gleichbreite Streifen angenähert werden (siehe Abbildung).
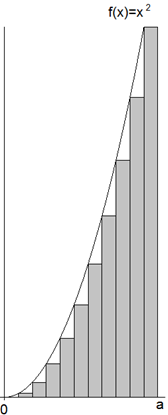
Wer jetzt bei gegebenem a den Taschenrechner oder bei variablem a ein Computer-Algebra-System einsetzt, erlebt nicht, wie die Integralformel \( \int\limits_{0}^{a} \)x2 dx=1/3·a3 zustande kommt. Auch für den eingangs zitierten Victor P. Habermann ist – trotz seiner Haltung zum elektronischen Werkzeug – diese Unterscheidung offenbar nicht deutlich geworden.